题目内容
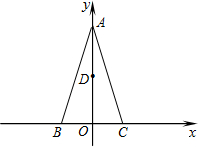 如图,△ABC在直角坐标系中,AB=AC,A(0,2
如图,△ABC在直角坐标系中,AB=AC,A(0,2| 2 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(0,
|
考点:勾股定理,根的判别式,坐标与图形性质
专题:压轴题
分析:假设P在AD的速度为3,在CD的速度为1,首先表示出总的时间,再根据根的判别式求出t的取值范围,进而求出D的坐标.
解答:解:假设P在AD的速度为3,在CD的速度为1,
设D坐标为(0,y),则AD=2
-y,CD=
=
,
∴设t=
+
,
等式变形为:t+
y-
=
,则t的最小值时考虑y的取值即可,
∴t2+(
y-
)t+(
y-
)2=y2+1,
∴
y2+(
-
t)y-t2+
t+1=0,
△=(
-
t)2-4×
(-t2+
t+1)≥0,
∴t的最小值为
,
∴y=
,
∴点D的坐标为(0,
),
故选D.
设D坐标为(0,y),则AD=2
| 2 |
| y2+12 |
| y2+1 |
∴设t=
2
| ||
| 3 |
| y2+1 |
等式变形为:t+
| 1 |
| 3 |
2
| ||
| 3 |
| y2+1 |
∴t2+(
| 2 |
| 3 |
4
| ||
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
∴
| 8 |
| 9 |
4
| ||
| 9 |
| 2 |
| 3 |
4
| ||
| 3 |
△=(
4
| ||
| 9 |
| 2 |
| 3 |
| 8 |
| 9 |
4
| ||
| 3 |
∴t的最小值为
| 3 |
∴y=
| ||
| 4 |
∴点D的坐标为(0,
| ||
| 4 |
故选D.
点评:本题考查了勾股定理的运用、一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况以及坐标于图形的性质题目的综合性较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥CD,AC与BD相交于点O,AB=3,若BO:BD=1:3,则CD等于
如图,AB∥CD,AC与BD相交于点O,AB=3,若BO:BD=1:3,则CD等于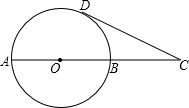 如图,在⊙O中,过直径AB延长线上的点C作⊙O的一条切线,切点于D,若AC=10,AB=6,则sinC的值为
如图,在⊙O中,过直径AB延长线上的点C作⊙O的一条切线,切点于D,若AC=10,AB=6,则sinC的值为