题目内容
已知△ABC的三边为a、b、c,且a+b=4,ab=1,c=
,试判定△ABC的形状.
| 14 |
考点:勾股定理的逆定理
专题:
分析:先利用完全平方公式得出a2+b2=(a+b)2-2ab=14=c2,再根据勾股定理的逆定理即可判断△ABC为直角三角形.
解答:解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2×1=14,
∵c=
,
∴c2=14,
∴a2+b2=c2,
∴△ABC为直角三角形.
∴a2+b2=(a+b)2-2ab=16-2×1=14,
∵c=
| 14 |
∴c2=14,
∴a2+b2=c2,
∴△ABC为直角三角形.
点评:本题考查了完全平方公式,勾股定理的逆定理,难度适中.正确求出a2+b2=14是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
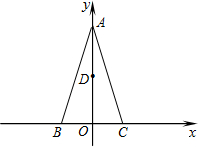 如图,△ABC在直角坐标系中,AB=AC,A(0,2
如图,△ABC在直角坐标系中,AB=AC,A(0,2| 2 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(0,
|
 如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE.求证:(1)AD平分∠BAC;(2)AE=AF.
如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE.求证:(1)AD平分∠BAC;(2)AE=AF. 如图所示:三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC,已知公路的造价2600万元/km,求修这条公路的最低造价是多少?
如图所示:三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC,已知公路的造价2600万元/km,求修这条公路的最低造价是多少?