题目内容
5.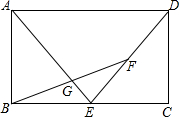 如图,已知矩形ABCD中,AB=8,BC=12,点E、F分别为线段BC、DE的中点,连接BF、AE交于点G.
如图,已知矩形ABCD中,AB=8,BC=12,点E、F分别为线段BC、DE的中点,连接BF、AE交于点G.(1)求线段BF的长度;
(2)求证:BG=GF.
分析 (1)过F作FM⊥BC于M,根据矩形的性质求出CD,求出FM=$\frac{1}{2}$DC=4,求出EM,根据勾股定理求出即可;
(2)延长BF、AD交于Q,过F作FW∥AD交AB于W,交AE于R,求出W为AB中点,R为AE中点,F为BQ的中点,根据三角形中位线求出FR,再证△DFQ∽△EFB,求出BE=DQ,求出FW,求出FR=BE,证△FRG∽△BEG,得出比例式,即可得出答案.
解答 (1)解:如图1: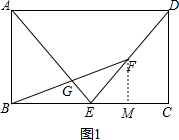
过F作FM⊥BC于M,
∵四边形ABCD是矩形,
∴AB=DC=8,∠C=90°,
∴∠FMB=∠C=90°,
∴FM∥DC,
∵F位DE的中点,
∴M为EC的中点,
∴FM=$\frac{1}{2}$DC=4,
∵E位BC中点,M为CE中点,
∴BE=EC=$\frac{1}{2}$BC=$\frac{1}{2}×12$=6,EM=EC=3,
∴BM=6+3=9,
在Rt△BMF中,由勾股定理得:BF=$\sqrt{{9}^{2}+{4}^{2}}$=$\sqrt{97}$;
(2)证明:如图2: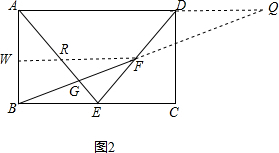
∵四边形ABCD是矩形,
∴AD=BC=12,AD∥BC,
延长BF、AD交于Q,过F作FW∥AD交AB于W,交AE于R,
∵F为DE中点,AD∥BC,
∴W为AB中点,R为AE中点,F为BQ的中点,
∴WR=$\frac{1}{2}$BE=$\frac{1}{2}×6$=3,
∵AD∥BC,
∴△DFQ∽△EFB,
∴$\frac{DQ}{BE}$=$\frac{EF}{DF}$,
∵DF=EF,
∴BE=DQ=6,
∴WF=$\frac{1}{2}$AQ=$\frac{1}{2}×$(12+6)=9,
∴RF=9-3=6=BE,
∵FW∥AD∥BC,
∴△FRG∽△BEG,
∴$\frac{FR}{BE}$=$\frac{FG}{BG}$,
∵BE=FR,
∴BG=GF.
点评 本题考查了三角形的中位线,矩形的性质,平行线的性质,相似三角形的性质和判定的应用,能正确作出辅助线是解此题的关键,题目综合性比较强,难度偏大.

 是方程
是方程 的解,则
的解,则 _______________.
_______________.
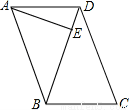
 已知平面直角坐标系内点A(m,n),将点A向上平移4个单位,向左平移1个单位得到点B,再向下平移2个单位,向左平移3个单位得到点C,再将C向上平移3个单位,向右平移7个单位得到点D,且D(2n,2-4m),连接直线AC,DC,AB,BD,得到如图所示.
已知平面直角坐标系内点A(m,n),将点A向上平移4个单位,向左平移1个单位得到点B,再向下平移2个单位,向左平移3个单位得到点C,再将C向上平移3个单位,向右平移7个单位得到点D,且D(2n,2-4m),连接直线AC,DC,AB,BD,得到如图所示.