题目内容
8.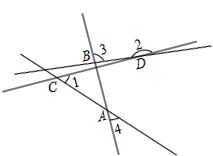 已知平面直角坐标系内点A(m,n),将点A向上平移4个单位,向左平移1个单位得到点B,再向下平移2个单位,向左平移3个单位得到点C,再将C向上平移3个单位,向右平移7个单位得到点D,且D(2n,2-4m),连接直线AC,DC,AB,BD,得到如图所示.
已知平面直角坐标系内点A(m,n),将点A向上平移4个单位,向左平移1个单位得到点B,再向下平移2个单位,向左平移3个单位得到点C,再将C向上平移3个单位,向右平移7个单位得到点D,且D(2n,2-4m),连接直线AC,DC,AB,BD,得到如图所示.(1)求n,m的值;
(2)请运用平行线的性质说明:∠1+∠2+∠3+∠4=360°;
(3)若有一动点E(a,b),其横、纵坐标a,b分别同时满足三个条件$\left\{\begin{array}{l}{a≥-4}\\{b≥2}\\{a+b≤0}\end{array}\right.$,请你在平面直角坐标系内画出点E(a,b)可能运动的范围,用阴影部分标注,并求出其阴影部分的面积.
分析 (1)根据横坐标右移加,左移减;纵坐标上移加,下移减可得关于n,m的二元一次方程组,解方程组即可求解;
(2)过C点作JF∥AB,交BD于E,过D点作GH∥AB,根据平行线的性质即可求得;
(3)根据题意在坐标系中,画出点E可能运动的范围是RT△ABC,根据三角形面积公式即可求得.
解答 解:(1)由题意得$\left\{\begin{array}{l}{m-1-3+7=2n}\\{n+4-2+3=2-4m}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=1}\end{array}\right.$.
故n的值为1,m的值为-1;
(2)如图1,过C点作JF∥AB,交BD于E,过D点作GH∥AB,
∴∠3=∠BEJ,∠BDG=∠BEC,∠GDK=∠ECB,∠CAB=∠ACF,
∠BEJ+∠BEC=180°,∠∠ECB+∠1+∠ACF=180°,
∴∠3+∠BDG+∠GDK+∠1+∠CAB=360°,
∵∠4=∠CAB,∠BDG+∠GDK=∠2,
∴∠1+∠2+∠3+∠4=360°;
(3)根据题意画出点E可能运动的范围是△ABC,如图2所示:
S阴影=$\frac{1}{2}$×2×2=2.
点评 本题考查了坐标和图形的关系,平行线的性质,三角形的面积,根据题意作出图形是解题的关键.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
17.等边三角形的边长为6,则它的面积是( )
| A. | 18$\sqrt{2}$ | B. | 9$\sqrt{2}$ | C. | 18$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
 )2·(-
)2·(- )=-
)=- 3 B.
3 B.  C.
C.  7÷
7÷ 7=1 D. 2
7=1 D. 2 4·3
4·3 2=6
2=6 8
8 ,则
,则 _______________.
_______________.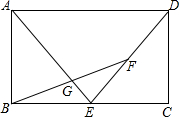 如图,已知矩形ABCD中,AB=8,BC=12,点E、F分别为线段BC、DE的中点,连接BF、AE交于点G.
如图,已知矩形ABCD中,AB=8,BC=12,点E、F分别为线段BC、DE的中点,连接BF、AE交于点G. 定义:在平面直角坐标系xOy中,给定两点M(xM,yM),N(xN,yN),对于给定的实数a,b,作a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),例如:d2,3((1,0),(4,7))=2|1-4|+3|0-7|=27.
定义:在平面直角坐标系xOy中,给定两点M(xM,yM),N(xN,yN),对于给定的实数a,b,作a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),例如:d2,3((1,0),(4,7))=2|1-4|+3|0-7|=27.