题目内容
10. 如图,直线AB切⊙O于点B,连接OA交⊙O于点C,点P为优弧$\widehat{BC}$上任意一点,若?A=30°,则∠P=30°.
如图,直线AB切⊙O于点B,连接OA交⊙O于点C,点P为优弧$\widehat{BC}$上任意一点,若?A=30°,则∠P=30°.
分析 由AB是切线得∠AOB=90°,由∠A=30°得∠AOB=60°,根据∠P=$\frac{1}{2}$∠AOB即可求出∠P.
解答 解:∵AB是切线,B是切点,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=90°-∠A=60°,
∵∠P=$\frac{1}{2}$∠AOB,
∴P=30°.
点评 本题考查切线的性质、圆周角的性质、直角三角形两个锐角互余,熟练记住圆的有关性质定理是解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
18.∠A是△ABC的一个内角,并且方程x2-4x•sin$\frac{A}{2}$+1=0的一根是$\sqrt{2}$-1,则∠A是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15. 如图,AB为⊙O的直径,弦CD⊥AB于H,弦CE⊥BD于G,交AB于点F,下列结论不正确的是( )
如图,AB为⊙O的直径,弦CD⊥AB于H,弦CE⊥BD于G,交AB于点F,下列结论不正确的是( )
 如图,AB为⊙O的直径,弦CD⊥AB于H,弦CE⊥BD于G,交AB于点F,下列结论不正确的是( )
如图,AB为⊙O的直径,弦CD⊥AB于H,弦CE⊥BD于G,交AB于点F,下列结论不正确的是( )| A. | CH=DH | B. | AH=FH | C. | CD=CE | D. | CF=DE |
 若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,若四边形BCED的面积是2,则△ADE的面积是$\frac{8}{5}$.
若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,若四边形BCED的面积是2,则△ADE的面积是$\frac{8}{5}$. 已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°,则△EDM的面积为$\sqrt{3}$.
已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°,则△EDM的面积为$\sqrt{3}$.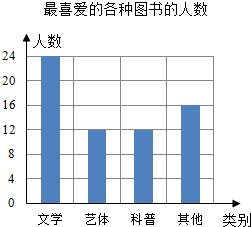 某校“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如图所示的条形统计图,则被调查的学生中喜爱文学类、艺体类、科普类的共有48人.
某校“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如图所示的条形统计图,则被调查的学生中喜爱文学类、艺体类、科普类的共有48人. 如图,△ABC中,∠ABC=90°,∠C=30°,AD是角平分线,DE⊥AC于E,AD、BE相交于点F,则图中的等腰三角形有( )
如图,△ABC中,∠ABC=90°,∠C=30°,AD是角平分线,DE⊥AC于E,AD、BE相交于点F,则图中的等腰三角形有( ) 如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.
如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.