题目内容
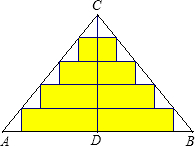
△ABC是一张等腰直角三角形纸板，∠C=90°，AC=BC=2，要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法如图所示，甲种剪法得到正方形ECFD的面积记为S1，乙种剪法得到正方形QPNM的面积记为S2，比较甲、乙两种剪法，哪种剪法所得的正方形面积更大？下面说法正确的是（ ）分析：分别求出甲、乙两种剪法所得的正方形面积，进行比较即可．
解答：解：如图甲，由题意，得AE=DE=EC，即EC=1，S正方形CFDE=12=1
如图乙，设MN=x，则由题意，得AM=MQ=PN=NB=MN=x，
∴3x=2
，
解得x=
，
∴S正方形PNMQ=（
）2=
，
又∵1＞
，
∴甲种剪法所得的正方形面积更大．
故选A．
如图乙，设MN=x，则由题意，得AM=MQ=PN=NB=MN=x，
∴3x=2
| 2 |
解得x=
2
| ||
| 3 |
∴S正方形PNMQ=（
2
| ||
| 3 |
| 8 |
| 9 |
又∵1＞
| 8 |
| 9 |
∴甲种剪法所得的正方形面积更大．
故选A．
点评：本题考查了正方形的性质，勾股定理，等腰直角三角形的性质，得出甲、乙两种剪法，所得的正方形面积是解题的关键．
练习册系列答案
相关题目
如图，△ABC是一张等腰直角三角形彩色纸，AC=BC=40cm．
