题目内容
已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为S1,则S1=
;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为S2,则S2=
;在余下的4个三角形中再按照小林设计的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为S3;按照同样的方法继续操作下去…,第n次裁剪得到
.

(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为S1,则S1=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
2n-1
2n-1
个新的正方形,它们的面积的和Sn=| 1 |
| 2n+1 |
| 1 |
| 2n+1 |

分析:(1)利用斜边长的
,向斜边作垂线得出正方形即可;
(2)根据题意,可求得S1,S2,S3,同理可得规律:Sn即是第n次剪取后面积和,根据此规律求解即可答案.
| 1 |
| 3 |
(2)根据题意,可求得S1,S2,S3,同理可得规律:Sn即是第n次剪取后面积和,根据此规律求解即可答案.
解答: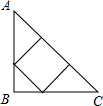 解:(1)如图所示;
解:(1)如图所示;
(2)∵四边形DBFE是正方形,
∴DE=EF=BF=DE,∠EFC=∠ADE=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴AD=DE=EF=CF=BF=BD=EF,
∵AB=BC=1,
∴DE=EF=
,
∴S正方形DBFE=S1=
×
=
;
同理:S2即是第二次剪取后的面积和,
Sn即是第n次剪取后的面积和,
∴第一次剪取后的面积和为:S1=
=
,
第二次剪取后的面积和为:S2=
×
×2=
=
,
第三次剪取后剩余三角形面积和为:S3=
×
×4=
=
,
…
第n次剪取后面积和为:Sn=
×
×2n-1=
.
故答案为:
,
,2n-1,
.
 解:(1)如图所示;
解:(1)如图所示;(2)∵四边形DBFE是正方形,
∴DE=EF=BF=DE,∠EFC=∠ADE=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴AD=DE=EF=CF=BF=BD=EF,
∵AB=BC=1,
∴DE=EF=
| 1 |
| 2 |
∴S正方形DBFE=S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
同理:S2即是第二次剪取后的面积和,
Sn即是第n次剪取后的面积和,
∴第一次剪取后的面积和为:S1=
| 1 |
| 22 |
| 1 |
| 4 |
第二次剪取后的面积和为:S2=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 23 |
| 1 |
| 8 |
第三次剪取后剩余三角形面积和为:S3=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 24 |
| 1 |
| 16 |
…
第n次剪取后面积和为:Sn=
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n+1 |
故答案为:
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n+1 |
点评:此题主要考查了图形的剪拼和正方形的性质以及图形变化规律等知识,注意得出图形变化规律是解题关键.

练习册系列答案
相关题目
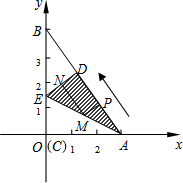 AB边上,记为D点,AE为折痕,E在y轴上.
AB边上,记为D点,AE为折痕,E在y轴上.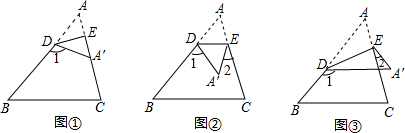
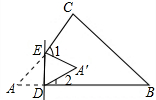 如图,已知△ABC是一张纸片,把∠A沿DE折叠,点A落在A′的位置,当∠1+∠2=100°时,则∠A的度数=
如图,已知△ABC是一张纸片,把∠A沿DE折叠,点A落在A′的位置,当∠1+∠2=100°时,则∠A的度数=