Question

14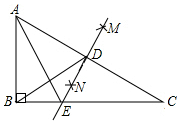．如图，在Rt△ABC中，∠B=90°，分别以A、C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧相交于点M、N，作直线MN，与AC交于点D，与BC交于点E，连接
AE．
（1）∠ADE=90°；
（2）AD=CD（填“＞、＜、=”）；
（3）AB=3，BC=4，AC=5时，△ABE的周长是7．

Answer 1

分析 （1）根据直线MN的画法可知直线MN垂直平分线段AC，由此即可得出∠ADE的度数；
（2）由（1）可知直线MN垂直平分线段AC，根据垂直平分线的性质即可得出AD=CD；
（3）由垂直平分线的性质可得出AE=CE，再根据三角形的周长以及AB、BC的长度即可得出结论．

解答 解：（1）∵分别以A、C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧相交于点M、N，作直线MN，
∴直线MN垂直平分线段AC，
∴∠ADE=90°．
故答案为：90．
（2）∵直线MN垂直平分线段AC，且MN与AC交于点D，
∴点D为线段AC的中点，
∴AD=CD．
故答案为：=．
（3）∵MN垂直平分线段AC，
∴AE=CE，
∵AB=3，BC=4，
∴C_△ABE=AB+BE+AE=AB+（BE+CE）=AB+BC=3+4=7．
故答案为：7．

点评 本题考查了垂直平分线的性质以及三角形的周长，根据直线MN的画法找出直线MN垂直平分线段AC是解题的关键．