Question

4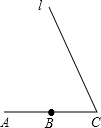．如图，AC=4，点B是线段AC的中点，直线l过点C且与AC的夹角为60°，则直线l上有点P，使得∠APB=30°，则PC的长为4或2．

Answer 1

分析 过点B作AC的垂线交直线l于点P，作AP′⊥直线l于点P′，根据线段垂直平分线的性质、直角三角形的性质解答即可．

解答 解：过点B作AC的垂线交直线l于点P，
则直线PB是线段AC的垂直平分线，
∴PA=PC，又直线l过点C且与AC的夹角为60°，
∴△PAC是等边三角形，
∵AB=BC，
∴∠APB=$\frac{1}{2}$∠APC=30°，
∴PC=PA=2AB=4，
作AP′⊥直线l于点P′，
∵AB=BC，
∴P′B=BC，又直线l过点C且与AC的夹角为60°，
∴△P′BC是等边三角形，
∴P′C=BC=2，
故答案为：4或2．

点评 本题考查的是线段的垂直平分线的性质和直角三角形的性质，掌握直角三角形斜边的中线等于斜边的一半是解题的关键，解答时，注意分情况讨论思想的应用．