题目内容

5．若α，β是方程x2+2x-2018=0的两个实数根，则α2+3α+β的值为（　　）
A．2015B．-2016C．2016D．2019

分析 根据方程的解得概念可得α2+2α=2018，由根与系数的关系可得α+β=-2，再代入α2+3α+β=α2+2α+α+β即可得．

解答 解：∵α，β是方程x2+2x-2018=0的两个实数根，
∴α2+2α-2018=0，即α2+2α=2018，α+β=-2，
则α2+3α+β=α2+2α+α+β=2018-2=2016，
故选：C．

点评 本题主要考查方程的解得概念及韦达定理，熟练掌握韦达定理是解题的关键．

练习册系列答案
相关题目
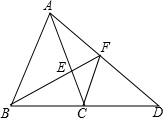15．如图，在三角形ABC中，AB=AC，点D在BC延长线上，点E在AC上，连接AD，连接BE并延长，交AD于F，连接FC，已知∠EBC=∠D．
（1）求证：AD•BC=BD•BE；
（2）点E在AC上什么位置时，FC垂直于BD？并证明．
16．已知二次函数y=ax2+bx+c的对称轴为直线x=2，且经过点（1，4），（0，$\frac{5}{2}$），求二次函数的解析式．
13．某班男生平均身高为160cm，高于平均身高记为正，低于平均身高记为负，若甲、乙学生的身高分别记为-5cm、+1cm，则乙学生比甲学生高6cm．
20．在-2，$\frac{3}{4}$，$\sqrt{\frac{4}{9}}$，-$\sqrt{2}$，$\frac{\sqrt{5}}{2}$这些数中，整数有-2，分数有$\frac{3}{4}$，$\sqrt{\frac{4}{9}}$，有理数有-2，$\frac{3}{4}$，$\sqrt{\frac{4}{9}}$，无理数有-$\sqrt{2}$，$\frac{\sqrt{5}}{2}$．
10．计算1+$\frac{1}{2}$×2-$\frac{1}{3}$÷3的结果是（　　）
A．1B．1$\frac{8}{9}$C．1D．$\frac{8}{9}$
17．计算：
（1）（-12）×（-5）=60；（2）（-$\frac{1}{3}$）×$\frac{1}{5}$=-$\frac{1}{15}$；
（3）（-4）×（-$\frac{1}{4}$）=1；（4）（-8.5）×3.14×0×（-2.72）=0；
（5）（-3）×$\frac{1}{2}$×（-$\frac{1}{4}$）=$\frac{3}{8}$；（6）（-1）×（-1）×（-1）=-1．
14．$\sqrt{a}$的算术平方根是3，b的立方根是-2，则a-b=89．
1．已知二次函数y=x2+bx+c的图象经过点A（-1，12）、B（2，-3）．求此抛物线的关系式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网