题目内容
13.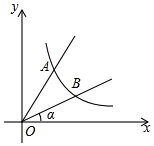 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为a,tana=$\frac{1}{2}$.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为a,tana=$\frac{1}{2}$.(1)求k的值及点B坐标.
(2)设点P是x轴上一动点.则当△PAB的面积为2时,求P点坐标.
分析 (1)把点A(1,a)代入y=2x,求出a=2,再把A(1,2)代入y=$\frac{k}{x}$,即可求出k的值;过B作BC⊥x轴于点C.在Rt△BOC中,由tanα=$\frac{1}{2}$,可设B(2h,h).将B(2h,h)代入y=$\frac{2}{x}$,求出h的值,即可得到点B的坐标;
(2)由A(1,2),B(2,1),利用待定系数法求出直线AB的解析式为y=-x+3,那么直线AB与x轴交点D的坐标为(3,0).设点P的坐标为(m,0),根据△PAB的面积为2列出方程$\frac{1}{2}$|3-m|×(2-1)=2,解方程即可求出m的值,可得P的坐标.
解答 解:(1)把点A(1,a)代入y=2x,
得a=2,
则A(1,2).
把A(1,2)代入y=$\frac{k}{x}$,得k=1×2=2;
过B作BC⊥x轴于点C.
∵在Rt△BOC中,tanα=$\frac{1}{2}$,
∴可设B(2h,h).
∵B(2h,h)在反比例函数y=$\frac{2}{x}$的图象上,
∴2h2=2,解得h=±1,
∵h>0,∴h=1,
∴B(2,1);
(2))∵A(1,2),B(2,1),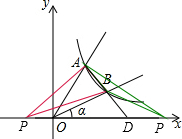
∴直线AB的解析式为y=-x+3,
设直线AB与x轴交于点D,则D(3,0).
∵S△PAB=S△PAD-S△PBD=2,
设点P的坐标为(m,0),
∴$\frac{1}{2}$|3-m|×(2-1)=2,
解得m1=-1,m2=7,
∴P点的坐标为(-1,0)或(7,0).
点评 本题考查了反比例函数与一次函数的交点问题,一次函数、反比例函数图象上点的坐标特征,利用待定系数法求反比例函数与一次函数的解析式,正切函数的定义,三角形的面积,难度适中,利用数形结合是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
16.某公司共25名员工,下表是他们月收入的资料.
(1)该公司员工月收入的中位数是3400元,众数是3000元.
(2)根据上表,可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
| 月收入/元 | 45000 | 18000 | 10000 | 5500 | 4800 | 3400 | 3000 | 2200 |
| 人数 | 1 | 1 | 1 | 3 | 6 | 1 | 11 | 1 |
(2)根据上表,可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
18. 如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.
如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.
(1)画出△ABC关于直线l成轴对称△A1B1C;
(2)将△ABC以点A为旋转中心逆时针旋转90°,画出旋转后的△AB2C2.
 如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.
如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.(1)画出△ABC关于直线l成轴对称△A1B1C;
(2)将△ABC以点A为旋转中心逆时针旋转90°,画出旋转后的△AB2C2.
2.甲工程队完成一项工程需n天,乙工程队要比甲工程队多用3天才能完成这项工程,那么两队共同工作一天完成这项工作的( )
| A. | $\frac{n}{n+3}$ | B. | $\frac{1}{n+3}$ | C. | $\frac{n}{2n+3}$ | D. | $\frac{1}{n}$+$\frac{1}{n+3}$ |
3.下列运算正确的是( )
| A. | a2+a3=a5 | B. | 6a5÷(-2a3)=-3a2 | C. | (-a3)2=-a6 | D. | (a-b)2=a2-b2 |
 如图所示的⊙O中,若∠DBC=∠BAC=30°,则∠BDO=30°.
如图所示的⊙O中,若∠DBC=∠BAC=30°,则∠BDO=30°.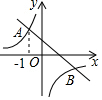 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$图象与一次函数y=kx+b的图象的2个交点分别为A(-1,n),B(2,n-3)
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$图象与一次函数y=kx+b的图象的2个交点分别为A(-1,n),B(2,n-3)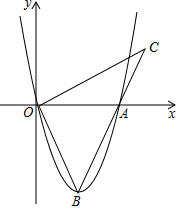 如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.
如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.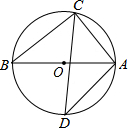 如图,已知AB是⊙O的直径,∠D=42°,则∠CAB的度数为48°.
如图,已知AB是⊙O的直径,∠D=42°,则∠CAB的度数为48°.