题目内容
8. 如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.(1)求线段MN的长.
(2)若C为线段AB上任意一点,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在AB的延长线上,且AB=acm,其它条件不变,MN的长度为$\frac{1}{2}a$(直接写出答案)
分析 (1)依据线段中点的定义进行计算即可;
(2)由线段中点的定义可知MC=$\frac{1}{2}AC$,CN=$\frac{1}{2}BC$,从而得到MC+NC=$\frac{1}{2}$(AC+BC),从而可求得MN的长度;
(3)先根据题意画出图形,然后由线段中点的定义可知MC=$\frac{1}{2}$CM=$\frac{1}{2}(a+BC)$,NC=$\frac{1}{2}BC$,由MN=MC-NC求解即可.
解答 解:(1)∵点M是AC的中点,
∴MC=$\frac{1}{2}AC$=$\frac{1}{2}×8$=4cm.
∵点N是BC的中点,
∴CN=$\frac{1}{2}BC$=$\frac{1}{2}×6$=3cm.
∴MN=MC+NC=4+3=7cm.
(2)∵点M是AC的中点,
∴MC=$\frac{1}{2}AC$.
∵点N是BC的中点,
∴CN=$\frac{1}{2}BC$.
∴MN=MC+NC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}×$14=7.
(3)如图所示: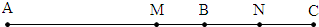
∵点M是AC的中点,
∴MC=$\frac{1}{2}AC$=$\frac{1}{2}$(a+BC).
∵点N是BC的中点,
∴CN=$\frac{1}{2}BC$.
∴MN=MC-NC=$\frac{1}{2}$(a+BC)-$\frac{1}{2}$BC=$\frac{1}{2}a$.
点评 本题主要考查的是两点之间的距离,掌握图形间线段之间的和差关系是解题的关键.

练习册系列答案
相关题目
17.估计31的立方根在哪两个整数之间( )
| A. | 2与3 | B. | 3与4 | C. | 4与5 | D. | 5与6 |
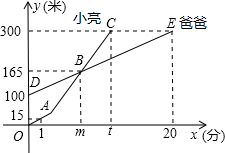 小亮和爸爸登山,两人距离地面的高度y(米)与小亮登山时间x(分)之间的函数图象分别如图中折线OA-AC和线段DE所示,根据函数图象进行以下探究:
小亮和爸爸登山,两人距离地面的高度y(米)与小亮登山时间x(分)之间的函数图象分别如图中折线OA-AC和线段DE所示,根据函数图象进行以下探究: