题目内容
4.阅读下面部分解题和探究思路,请补充完整并完成相关任务.[原题]如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.
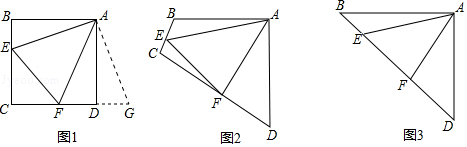
(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°
∴点F、D、G在一条直线上,根据SAS,易证△AFG≌△AFE
∴GF=EF,从而可得EF=BE+DF
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,且∠EAF=45°,若∠B、∠D都不是直角,则当∠B与∠D满足等量关系∠B+∠D=180°时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABD中,AB=AD,∠BAD=90°,点E、F均在边BD上,且∠EAF=45°,据图形提示试猜想BE、FE、DF满足的等量关系,并写出推理过程.
分析 (1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,再证明△AFG≌△AFE进而得到EF=FG,即可得EF=BE+DF;
(2)∠B+∠D=180°时,EF=BE+DF,与(1)的证法类同;
(3)把△AFD绕点A顺时针旋转90°得到△AEE′,连接EE′,根据旋转的性质,可知△AFD≌△ABE′得到BE′=FD,AE′=AF,∠D=∠ABE′,∠EAD=∠E′AB,在Rt△ABD中的,AB=AD,可求得∠E′BD=90°,所以E′B2+BE2=E′E2,证△AE′E≌△AE′F,利用FE=EE′得到EF2=BE2+FD2.
解答 解:(1)∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$
∴△AFE≌△AFG(SAS),
∴EF=FG,
即EF=BE+DF,
故答案为:△AFE;
(2)当∠B+∠D=180°时,EF=BE+DF,如图2
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$
∴△AFE≌△AFG(SAS),
∴EF=FG,
即EF=BE+DF,
故答案为:∠B+∠D=180°;
(3)猜想:EF2=BE2+FD2,
证明:把△AFD绕点A顺时针旋转90°得到△AEE′,连接EE′,如图3,
∴△AFD≌△ABE′,
∴BE′=FD,AE′=AF,∠D=∠ABE′,∠EAD=∠E′AB,
∵AB=AD,
∴∠ABD=∠ADB=45°,
∴∠ABD+∠ABE′=90°,即∠E′BD=90°,
∴E′B2+BE2=E′E2,
又∵∠FAE=45°,
∴∠BAE+∠EAD=45°,
∴∠E′AB+∠BAE=45°,即∠E′AE=45°,
在△AEE′和△AEF中
$\left\{\begin{array}{l}{AE=AE}\\{∠E′AE=∠FAE}\\{AE′=AF}\end{array}\right.$
∴△AEE′≌△AEF(SAS),
∴EE′=FE,
∴EF2=BE2+DF2.
点评 本题为四边形的综合应用,涉及全等三角形的判定和性质、旋转变换的性质以及勾股定理及其逆定理的应用等知识.掌握全等三角形的判定定理和性质定理、灵活运用勾股定理的逆定理判断直角三角形是解题的关键.本题考查知识点较多,综合性较强,难度适中.

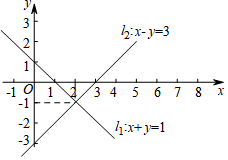 如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
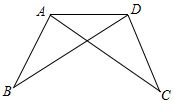 如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.
如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.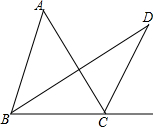 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=40°,则∠D的度数是20°.
如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=40°,则∠D的度数是20°.