题目内容
6.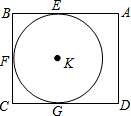 定义:定点A与⊙O上的任意一点之间的距离的最小值称为点A与⊙O之间的距离.现有一矩形ABCD如图,AB=6cm,BC=4cm,⊙K与矩形的边AB、BC、CD分别相切于点E、F、G,则点A与⊙K的距离为(2$\sqrt{5}$-2)cm.
定义:定点A与⊙O上的任意一点之间的距离的最小值称为点A与⊙O之间的距离.现有一矩形ABCD如图,AB=6cm,BC=4cm,⊙K与矩形的边AB、BC、CD分别相切于点E、F、G,则点A与⊙K的距离为(2$\sqrt{5}$-2)cm.
分析 连结KF、KE、KG、AK,AK交⊙O于M,如图,根据切线的性质得KE⊥AB,KF⊥BC,KG⊥CD,则可证明四边形BCGE为矩形得到EG=BC=4,再证明四边形BFKE为正方形得到BE=KF=2,所以AE=AB-BE=4,于是可根据勾股定理计算出AK=2$\sqrt{5}$,则AM=AK-KM=2$\sqrt{5}$-2,然后根据新定义即可得到点A与⊙K的距离.
解答 解:连结KF、KE、KG、AK,AK交⊙O于M,如图,
∵⊙K与矩形的边AB、BC、CD分别相切于点E、F、G,
∴KE⊥AB,KF⊥BC,KG⊥CD,
∵AB∥CD,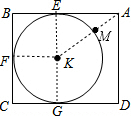
∴K、E、G三点共线,即EG为⊙O的直径,
∴四边形BCGE为矩形,
∴EG=BC=4,
∵KE=KF=2,
∴四边形BFKE为正方形,
∴BE=KF=2,
∴AE=AB-BE=6-2=4,
在Rt△AEK中,AK=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴AM=AK-KM=2$\sqrt{5}$-2,
∴点A与⊙K的距离为(2$\sqrt{5}$-2)cm.
故答案为(2$\sqrt{5}$-2)cm.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了新定义和矩形的性质.

练习册系列答案
相关题目
16.函数y=$\frac{1}{2}$x2-2x写成y=a(x-h)2+k的形式是( )
| A. | y=(x-1)2+2 | B. | y=$\frac{1}{2}$(x-2)2-2 | C. | y=$\frac{1}{2}(x-1)^{2}$+$\frac{1}{2}$ | D. | y=$\frac{1}{2}(x-2)^{2}$+3 |
1.计算-3-2的结果是( )
| A. | -1 | B. | 1 | C. | 5 | D. | -5 |
15.下列命题是假命题的是( )
| A. | 锐角小于90° | B. | 两直线平行,同位角相等 | ||
| C. | 若a=b,则a2=b2 | D. | 若a>b,则a2>b2 |