题目内容
如图，△ABC内接于⊙O，直径AD=2，∠ABC=30°，则CD的长度是考点：圆周角定理,解直角三角形
专题：
分析：根据圆周角定理求出∠D=∠B，∠ACD=90°，解直角三角形求出即可．
解答：解：∵∠ABC=30°，
∴∠D=∠ABC=30°，
∵AD为直径，
∴∠ACD=90°，
在Rt△ACD中，CD=AD×cos30°=2×
=
，
故答案为：
．
∴∠D=∠ABC=30°，
∵AD为直径，
∴∠ACD=90°，
在Rt△ACD中，CD=AD×cos30°=2×
| ||
| 2 |
| 3 |
故答案为：
| 3 |
点评：本题考查了圆周角定理和解直角三角形的应用，主要考查学生的推理能力和计算能力，题目比较典型，难度适中．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
如图，已知A（-2，n）B（3，-2）是一次函数y=kx+b的图象和反比例函数y=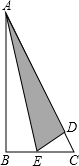
如图所示的三角形纸片中∠B=90°，AC=13，BC=5．现将纸片进行折叠，使得顶点B落在AC边上，折痕为AE．则BE的长为
如图，AB∥CD，∠ABE=60°，∠F=50°，则∠E的度数为