题目内容
如图,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为 cm2.


18【考点】等腰梯形的性质.菁优网版权所有
【分析】通过作辅助线,把等腰梯形ABCD的面积转化成直角三角形的面积来完成.
【解答】解:方法一:
过点B作BE∥AC,交DC的延长线于点E,又AB∥CE,
∴四边形ACEB是平行四边形,又等腰梯形ABCD
∴BE=AC=DB=6cm,AB=CE,
∵AC⊥BD,
∴BE⊥BD,
∴△DBE是等腰直角三角形,
∴S等腰梯形ABCD=

=
 =
=

=S△DBE=

=6×6÷2
=18(cm2).
方法二:
∵BD是△ADB和△CDB的公共底边,又AC⊥BD,
∴AC=△ADB的高﹢△CDB的高,
∴梯形ABCD的面积=△ADB面积+△CDB面积=
 BD×AC=6×
BD×AC=6×
 =18(cm2).
=18(cm2).
故答案为:18.


【点评】本题考查了梯形面积的计算,以及它的性质,还运用了转化的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 B.
B.


 D.
D.

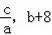
 ),求当x≥1时y1的取值范围.
),求当x≥1时y1的取值范围.
 B.
B.
 C.
C.




 ﹣1=( )
﹣1=( ) ,求代数式(b-c) 2-3(b-c)+
,求代数式(b-c) 2-3(b-c)+ 的值。
的值。