题目内容
 如图,△ABC与△ADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.
如图,△ABC与△ADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.考点:相似三角形的性质
专题:
分析:由△ABC与△ADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,可求得BC的长,然后分别从△ABC∽△ADB或△ABC∽△BDA,根据相似三角形的对应边成比例,即可求得答案.
解答:解:∵∠ABC=∠ADB=90°,AC=5cm,AB=4cm,
∴BC=
=3cm,
若△ABC∽△ADB,则
=
,
即
=
,
解得:AD=
cm;
若△ABC∽△BDA,则
=
,
即
=
,
解得:AD=
cm;
AD的长为:
cm或
cm.
∴BC=
| AC2-AB2 |
若△ABC∽△ADB,则
| AC |
| AB |
| AB |
| AD |
即
| 5 |
| 4 |
| 4 |
| AD |
解得:AD=
| 16 |
| 5 |
若△ABC∽△BDA,则
| AC |
| AB |
| BC |
| AD |
即
| 5 |
| 4 |
| 3 |
| AD |
解得:AD=
| 12 |
| 5 |
AD的长为:
| 16 |
| 5 |
| 12 |
| 5 |
点评:此题考查了相似三角形的性质.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若关于x的不等式kx2+(k-6)x+2>0的解为全体实数,则实数k的取值范围是( )
| A、-2<k<18 |
| B、-18<k<-2 |
| C、2<k<18 |
| D、-18<k<2 |
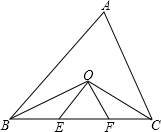 如图,△ABC的角平分线BO、CO交于点O,OE∥AB,OF∥AC,BC=10,①△OEF的周长=
如图,△ABC的角平分线BO、CO交于点O,OE∥AB,OF∥AC,BC=10,①△OEF的周长= 现有一张长为6.5cm,宽为2cm的纸片,如图,请你将它分割成6块,再拼合成一个正方形.(要求:先在图中画出分割线,再画出拼成的正方形并标明相应数据)
现有一张长为6.5cm,宽为2cm的纸片,如图,请你将它分割成6块,再拼合成一个正方形.(要求:先在图中画出分割线,再画出拼成的正方形并标明相应数据)