题目内容
16．一元二次方程2x（x-3）=0根的情况是（ ）| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 只有一个实数根 | D． | 没有实数根 |
分析 先把方程化为一元二次方程的一般形式，再根据根的判别式即可得出结论．
解答 解：∵一元二次方程2x（x-3）=0可化为2x2-6x=0，△=36＞0，
∴方程有两个不相等的实数根．
故选A．
点评 本题考查的是根的判别式，熟知一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac的关系是解答此题的关键．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
7．当x=-2011时，计算下列各式的值．
（1）$\frac{x-|x|}{2}$×$\frac{x+|x|}{2}$；
（2）$\frac{-x+|x|}{2}$÷$\frac{x-|x|}{2}$．
（1）$\frac{x-|x|}{2}$×$\frac{x+|x|}{2}$；
（2）$\frac{-x+|x|}{2}$÷$\frac{x-|x|}{2}$．
6．
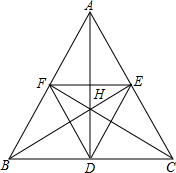如图，锐角△ABC的垂心为H，三条高的垂足分为D、E、F，则H是△DEF的（ ）
如图，锐角△ABC的垂心为H，三条高的垂足分为D、E、F，则H是△DEF的（ ）| A． | 垂心 | B． | 重心 | C． | 内心 | D． | 外心 |