题目内容
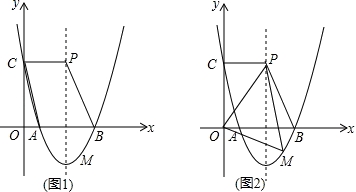
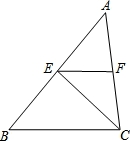
如图1,已知二次函数y=ax2﹣8ax+12(a>0)的图象与x轴分别交于A、B两点,与y轴交于点C,点P在抛物线的对称轴上,且四边形ABPC为平行四边形.
(1)求此抛物线的对称轴,并确定此二次函数的解析式;
(2)点M为x轴下方抛物线上一点,若△OMP的面积为36,求点M的坐标.
【考点】待定系数法求二次函数解析式;二次函数图象上点的坐标特征;平行四边形的性质.
【专题】计算题.
【分析】(1)利用二次函数的性质可得对称轴为直线x=4,则PC=4,再根据平行四边形的性质得PC=AB=4,然后利用抛物线的对称性可得A(2,0),B(6,0),然后把把点 A(2,0)代入得y=ax2﹣8ax+12求出a=1,所以二次函数解析式为y=x2﹣8x+12;
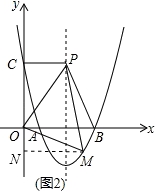
(2)根据二次函数图象上点的坐标特征,设M(m,x2﹣8x+12),其中2<m<6,作MN⊥y轴于N,如图2,利用S梯形CPMN﹣S△OCP﹣S△OMN=S△OPM得到 (4+m)(12﹣m2+8m﹣12)﹣
(4+m)(12﹣m2+8m﹣12)﹣ ×4×12﹣
×4×12﹣ m(﹣m2+8m﹣12)=36,化简得:m2﹣11m+30=0,然后解方程求出m即可得到点M的坐标.
m(﹣m2+8m﹣12)=36,化简得:m2﹣11m+30=0,然后解方程求出m即可得到点M的坐标.
【解答】解:(1)对称轴为直线x=﹣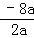 =4,则PC=4,
=4,则PC=4,
∵四边形ABPC为平行四边形,
∴PC∥AB,PC=AB,
∴PC=AB=4,
∴A(2,0),B(6,0),
把点 A(2,0)代入得y=ax2﹣8ax+12得4a﹣16a+12=0,解得a=1,
∴二次函数解析式为y=x2﹣8x+12;
(2)设M(m,x2﹣8x+12),其中2<m<6,
作MN⊥y轴于N,如图2,
∵S梯形CPMN﹣S△OCP﹣S△OMN=S△OPM,
∴ (4+m)(12﹣m2+8m﹣12)﹣
(4+m)(12﹣m2+8m﹣12)﹣ ×4×12﹣
×4×12﹣ m(﹣m2+8m﹣12)=36,
m(﹣m2+8m﹣12)=36,
化简得:m2﹣11m+30=0,解得m1=5,m2=6,
∴点M的坐标为(5,﹣3).
【点评】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案九年级(1)班数学活动选出甲、乙两组各10名学生,进行趣味数学答题比赛,共10题,答对题数统计如表一:
(表一)
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲组 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙组 | 0 | 0 | 4 | 3 | 2 | 1 |
(表二)
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲组 | 8 | 8 | 8 | 1.6 |
| 乙 | 8 | __________ | __________ | __________ |
(1)根据表一中统计的数据,完成表二;
(2)请你从平均数和方差的角度分析,哪组的成绩更好些?
阅读下列材料:
利用完全平方公式,可以将多项式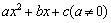 变形为
变形为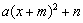 的形式, 我们把这样的变形方法叫做多项式
的形式, 我们把这样的变形方法叫做多项式 的配方法.
的配方法.
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如: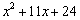 =
=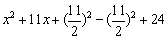
=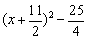
=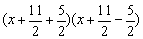
=
根据以上材料,解答下列问题:
(1)用多项式的配方法将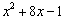 化成
化成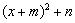 的形式;
的形式;
(2)下面是某位同学用配方法及平方差公式把多项式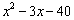 进行分解因式的解答过程:
进行分解因式的解答过程:
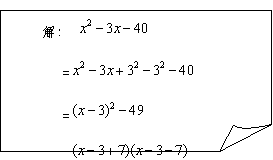 |
老师说,这位同学的解答过程中有错误,请你找出该同学解答中开始出现错误的地方,并用“ ”标画出来,然后写出完整的、正确的解答过程:
(3)求证:x,y取任何实数时,多项式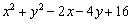 的值总为正数.
的值总为正数.
 能分解因式,其结果是
能分解因式,其结果是 ,
, = 。
= 。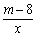 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
 B.
B. C.
C. D.
D.
 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是 .
的取值范围是 .