题目内容
如图,在△ABC中,E、F分别是AB、AC的中点,△CEF的面积为2.5,则△ABC的面积为__________.
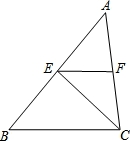
10.
【考点】三角形的面积.
【分析】由于E、F分别是AB、AC的中点,可知EF是△ABC的中位线,利用中位线的性质可知EF∥BC,且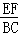 =
=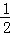 ,根据△AEF和△CEF是同底等高,△BCE和△CEF是同高,求得△AEF的面积为2.5,△BCE的面积为2.5×2=5,进而求得∴△ABC的面积等于10.
,根据△AEF和△CEF是同底等高,△BCE和△CEF是同高,求得△AEF的面积为2.5,△BCE的面积为2.5×2=5,进而求得∴△ABC的面积等于10.
【解答】解:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,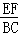 =
=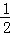 ,
,
∵△CEF的面积为2.5,
∵△AEF和△CEF是同底等高,△BCE和△CEF是同高,
∴△AEF的面积为2.5,△BCE的面积为2.5×2=5,
∴△ABC的面积等于10.
故答案为10.
【点评】本题考查了中位线的判定和性质以及三角形面积,求得△AEF和△CEF,△BCE和△CEF的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
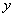 (cm2),运动时间为
(cm2),运动时间为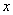 (秒),则下列图象中能大致反映
(秒),则下列图象中能大致反映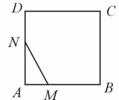
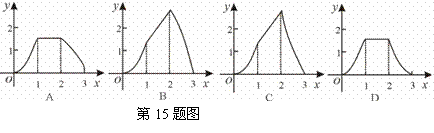

 B.2 C.
B.2 C. D.
D.
 ,当-2≤
,当-2≤ ≤3时,函数值
≤3时,函数值 的取值范围 是 .
的取值范围 是 .