题目内容
 已知:如图,在Rt△ABC中,∠C=90°,DC=1.点D为BC边上一点,且BD=2AD,∠DAC=30°,求斜边AB长(结果保留根号).
已知:如图,在Rt△ABC中,∠C=90°,DC=1.点D为BC边上一点,且BD=2AD,∠DAC=30°,求斜边AB长(结果保留根号).考点:解直角三角形
专题:
分析:解直角三角形求出AC和AD,求出BD,即可求出BC,根据勾股定理求出AB即可.
解答:解:∵在Rt△ABC中,∠C=90°,DC=1,∠DAC=30°,
∴AD=2DC=2,AC=
=
,
∵BD=2AD,
∴BD=4,
∴BC=5,
由勾股定理得:AB=
=
=2
.
∴AD=2DC=2,AC=
| DC |
| tan30° |
| 3 |
∵BD=2AD,
∴BD=4,
∴BC=5,
由勾股定理得:AB=
| BC2+AC2 |
52+(
|
| 7 |
点评:本题考查了含30度角的直角三角形性质,解直角三角形,勾股定理的应用,解此题的关键是求出AC、BC的长.

练习册系列答案
相关题目
当ab>0时,y=ax2与y=ax+b的图象大致是( )
A、 |
B、 |
C、 |
D、 |
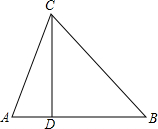 如图,已知△ABC中,AC=5,AB=6,BC=7,AB边上的高CD=3
如图,已知△ABC中,AC=5,AB=6,BC=7,AB边上的高CD=3
 已知:如图,∠ABC=∠ADC=90°,E、F分别是AC、BD的中点.求证:EF⊥BD.
已知:如图,∠ABC=∠ADC=90°,E、F分别是AC、BD的中点.求证:EF⊥BD.