��Ŀ����
��֪������y=Ax 2 +Bx+C��y�ύ�ڵ�A��0��3������x��ֱ���B��1��0����C��5��0������.
��1����������ߵĽ���ʽ��
��2������DΪ�߶�OA��һ�����ȷֵ㣬��ֱ��DC�Ľ���ʽ��
��3����һ������P��OA���е�M�������ȵ���x���ϵ�ij�㣨��Ϊ��E�����ٵ��������ߵĶԳ�����ij�㣨��Ϊ��F��������˶�����A.��ʹ��P�˶�����·����̵ĵ�E����F�����꣬�������������·���ij�.
��4������N������Ϊ��3��4����QΪx����һ�㣬��ONQΪ���������Σ���ֱ��д����Q�����ꡣ��14�֣�
��1�������ߵĽ���ʽΪ  ����2������D������Ϊ��0,1��ʱ��ֱ��CD�Ľ���ʽΪy=
����2������D������Ϊ��0,1��ʱ��ֱ��CD�Ľ���ʽΪy=  x+1; ����D������Ϊ��0,2��ʱ��ֱ��CD�Ľ���ʽΪy=
x+1; ����D������Ϊ��0,2��ʱ��ֱ��CD�Ľ���ʽΪy=  x+2.��3��
x+2.��3�� .��4��Q1��5,0��,Q2��-5,0��,Q3��
.��4��Q1��5,0��,Q2��-5,0��,Q3��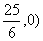 ,Q4��6,0��
,Q4��6,0��
��������
�����������1���������⣬C=3��
����
���
���������߽���ʽΪy= x2��
x2��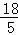 x+3��
x+3��
��2��������ɵ�OA�����ȷֵ�ֱ�Ϊ��0��1������0��2����
��ֱ��CD�Ľ���ʽΪy=kx+B��
����D������Ϊ��0��1��ʱ��ֱ��CD�Ľ���ʽΪy=�� x+1��
x+1��
����D������Ϊ��0��2��ʱ��ֱ��CD�Ľ���ʽΪy=�� x+2��
x+2��
��3����ͼ�������⣬�ɵ�M��0�� ����
����
�ߵ�M���M�����x��ĶԳƣ�
���ΪM�䣨0���� ����
����
���A���������߶Գ���x=3�ĶԳƵ�ΪA'��6��3����
����A'M'��
������Գ��Լ�������߶���̿�֪��A'M'�ij����������P�˶��������·���ij���
��A'M'��x��Ľ���Ϊ����E�㣬��ֱ��x=3�Ľ���Ϊ����F�㣮
������ֱ��A'M'�Ľ���ʽΪy= x��
x�� ��
��
��ɵ�E������Ϊ��2��0����F������Ϊ��3�� ����
����
�ɹ��ɶ�������� ��
��
���P�˶��������·����ME+EF+FA���ij�Ϊ ����8�֣�
����8�֣�

��4��Q1��5,0��,Q2��-5,0��,Q3��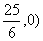 ,Q4��6,0��
,Q4��6,0��
���㣺���κ����ۺ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� ��-
��- ����-3 -
����-3 -


