题目内容
(本题满分10分)如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

(25+5 )km.
)km.
【解析】
试题分析:过B点作BE⊥l1,交l1于E,CD于F,l2于G.在Rt△ABE中,根据三角函数求得BE,在Rt△BCF中,根据三角函数求得BF,在Rt△DFG中,根据三角函数求得FG,再根据EG=BE+BF+FG即可求解.
试题解析:解:过B点作BE⊥l1,交l1于E,CD于F,l2于G.
在Rt△ABE中,BE=ABsin30°=20× =10km,
=10km,
在Rt△BCF中,BF=BC÷cos30°=10÷ =
= km,
km,
CF=BFsin30°= ×
× =
= km,
km,
DF=CD﹣CF=(30﹣ )km,
)km,
在Rt△DFG中,FG=DFsin30°=(30﹣ )×
)× =(15﹣
=(15﹣ )km,
)km,
∴EG=BE+BF+FG=(25+5 )km.
)km.
故两高速公路间的距离为(25+5 )km.
)km.

考点:解直角三角形的应用.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 =1
=1  与
与 轴交于A(-4,0)和B(1,0)两点,与
轴交于A(-4,0)和B(1,0)两点,与 轴交于点C.
轴交于点C.
 轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.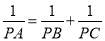 ;③ PA·PE=PB·PC.其中,正确结论的个数为( )。
;③ PA·PE=PB·PC.其中,正确结论的个数为( )。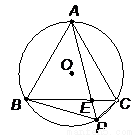
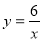 的图像上的是( )
的图像上的是( ) ;(2)化简:
;(2)化简: .
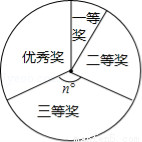
. _______.
_______.

 在实数范围内有意义,则x的取值范围是( ).
在实数范围内有意义,则x的取值范围是( ).