题目内容
(本题满分8分)
(1)计算: ;(2)化简:
;(2)化简: .
.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)根据实数的运算性质,首先计算乘方,化简二次根式和绝对值部分,然后合并;
(2)应用完全平方公式和乘法分配律展开,然后合并同类项.
试题解析:(1)解:原式=-1-1+2 +2-
+2- =
= .
.
(2)解:原式
 .
.
考点:实数的运算;整式的混合运算.
考点分析: 考点1:有理数 1、有理数的概念:正数和分数统称为有理数.2、有理数的分类:
①按整数、分数的关系分类; ②按正数、负数与0的关系分类.
有理数{整数{正整数0负整数分数{正分数负分数 有理数 {正数{正整数正分数0负数{负整数负分数
注意:如果一个数是小数,它是否属于有理数,就看它是否能化成分数的形式,所有的有限小数和无限循环小数都可以化成分数的形式,因而属于有理数,而无限不循环小数,不能化成分数形式,因而不属于有理数. 考点2:整式 (1)概念:单项式和多项式统称为整式.
他们都有次数,但是多项式没有系数,多项式的每一项是一个单项式,含有字母的项都有系数.
(2)规律方法总结:
①对整式概念的认识,凡分母中含有字母的代数式都不属于整式,在整式范围内用“+”或“-”将单项式连起来的就是多项式,不含“+”或“-”的整式绝对不是多项式,而单项式注重一个“积”字.
②对于“数”或“形”的排列规律问题,用先从开始的几个简单特例入手,对比、分析其中保持不变的部分及发展变化的部分,以及变化的规律,尤其变化时与序数几的关系,归纳出一般性的结论. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 -2x+6的值为9,则-2
-2x+6的值为9,则-2
 的图象如图所示,那么二次函数y=kx2-k2x-1的图象大致为( )
的图象如图所示,那么二次函数y=kx2-k2x-1的图象大致为( )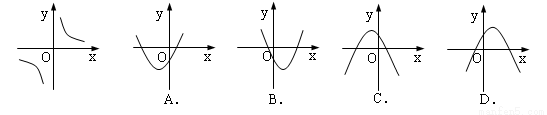

 的值为负数,则x的取值范围是 .
的值为负数,则x的取值范围是 .
 的值;
的值; 的值
的值