题目内容
4.观察下列各式:(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
根据前面各式的规律,你能不能得出下面式子的结果.
(x-1)(xn+xn-1+xn-2+…+x+1)=xn+1-1.(其中n为正整数)
分析 直接利用已知数据得出x的次数变化,进而得出答案.
解答 解:∵(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
∴(x-1)(xn+xn-1+xn-2+…+x+1)=xn+1-1.
故答案为:xn+1-1.
点评 此题主要考查了数字变化规律,根据已知得出x的次数变化规律是解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

 重合,折痕为EF.若AB=3cm,BC=5cm.
重合,折痕为EF.若AB=3cm,BC=5cm.

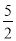 D. 2
D. 2 ;
;  ;
; ;
; .
.