题目内容
15.小明在长为400米的环形跑道上跑步,跑第二圈比第一圈平均速度增加了25%,这样跑第二圈所用时间比第一圈少用了30秒.求小明跑第一圈时的平均速度.分析 设小明跑第一圈时的平均速度为x米/秒,根据跑第二圈所用时间比第一圈少用了30秒建立方程,求解即可.
解答 解:设小明跑第一圈时的平均速度为x米/秒,根据题意得
$\frac{400}{x}$-$\frac{400}{(1+25%)x}$=30,
解得:x=$\frac{8}{3}$.
经检验,x=$\frac{8}{3}$是原方程的解,且符合题意.
答:小明跑第一圈时的平均速度为$\frac{8}{3}$米/秒.
点评 考查了分式方程的应用,列方程解应用题的关键是正确确定题目中的相等关系,根据相等关系确定所设的未知数,列方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.计算(-2a)2的结果是( )
| A. | -4a2 | B. | 2a2 | C. | -2a2 | D. | 4a2 |
20.长春市轻轨3号线开通以来,极大缓解了城市的交通压力,据统计,每天轻轨的运载人数为16600人次,16600这个数用科学记数法表示为( )
| A. | 16.6×103 | B. | 1.66×104 | C. | 166×102 | D. | 1.66×105 |
4.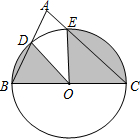 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )| A. | $\frac{64}{9}π$ | B. | $\frac{32}{9}π$ | C. | $\frac{16}{9}π$ | D. | $\frac{8}{9}π$ |
5.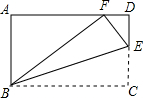 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
 如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.
如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.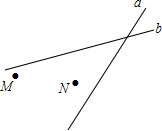 如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.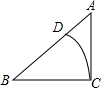 如图,Rt△ABC中,∠C=90°,∠A=50°,BC=3,以点B为圆心,BC为半径作弧,交AB于点D,则$\widehat{CD}$的长为$\frac{2π}{3}$.
如图,Rt△ABC中,∠C=90°,∠A=50°,BC=3,以点B为圆心,BC为半径作弧,交AB于点D,则$\widehat{CD}$的长为$\frac{2π}{3}$. 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.