题目内容
18．
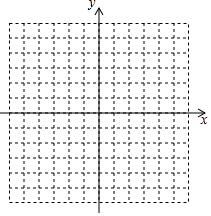在直角坐标平面内，点A的坐标为（3，2），点B与点A关于原点对称；点C的坐标为（3，4），点D与点C关于x轴对称（1）分别写出点B，点D的坐标，在图中的直角坐标平面内画出△ABD，并求其面积；
（2）如果点P（0，-6），试求△ABP的面积．
分析 （1）由关于原点、x轴对称点的坐标特点得出点B、点D的坐标，即可得出答案；
（2）由S△ABP=S△APO+S△BPO可得答案．
解答 解：（1）如图所示，△ABD即为所求，
点B（-3，-2）、D（3，-4），
由图可知，AD=6，AD边上的高为6，
则△ABD的面积为$\frac{1}{2}$×6×6=18；
（2）S△ABP=S△APO+S△BPO=$\frac{1}{2}$×6×3+$\frac{1}{2}$×6×3=18．
点评 本题主要考查作图-轴对称变换，熟练掌握轴对称变换的定义及其性质和割补法求三角形的面积是解题的关键．
练习册系列答案
相关题目
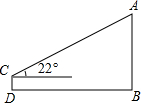如图，某校数学兴趣小组为了测得学校旗杆的高度AB，在点D处用高为1.2米的测角仪CD，测得旗杆顶端A的仰角为22°，又测得BD=30米，求这根旗杆的高度AB．（精确到0.1米）
已知三条线段h，m，c，求作△ABC，使其BC边上的高AH=h，中线AD=m，AB=c．