题目内容
5.若关于x的不等式2x-m≥0的负整数解为-1,-2,-3,则m的取值范围是( )| A. | -8<m≤-6 | B. | -6≤m<-4 | C. | -6<m≤-4 | D. | -8≤m<-6 |
分析 首先解不等式求得解集,然后根据不等式只有负整数解为-1,-2,-3,得到关于m的不等式,求得m的范围.
解答 解:解2x-m≥0得x>$\frac{m}{2}$.
则-4<$\frac{m}{2}$≤-3,
解得:-8<m≤-6.
故选A.
点评 此题比较简单,根据x的取值范围正确确定$\frac{m}{2}$的范围是解题的关键.再解不等式时要根据不等式的基本性质.

练习册系列答案
相关题目
20.下列二元一次方程组无解的是( )
| A. | $\left\{\begin{array}{l}{5x-3y=16}\\{3x-5y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x-y=1}\\{y=2x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=2}\\{2x-2y=-4}\end{array}\right.$ |
17.甲、乙、丙三个人站在一排,通过实验可得,甲站在中间的概率为( )
| A. | $\frac{1}{6}$ | B. | $\overline{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
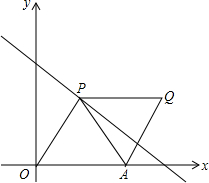 如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA.
如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA. 如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径为3.
如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径为3.