题目内容
19.已知正方形ABCD的边长为4$\sqrt{2}$,如果P是正方形内一点,且PA=PC=2$\sqrt{5}$,那么BP的长为6或2.分析 根据全是三角形的性质得到∠ABP=∠CBP=45°,过P作PE⊥BC于E,根据勾股定理即可得到结论.
解答 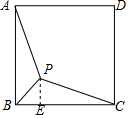 解:在△ABP与△CBP中,$\left\{\begin{array}{l}{AB=CB}\\{PB=PB}\\{AP=CP}\end{array}\right.$,
解:在△ABP与△CBP中,$\left\{\begin{array}{l}{AB=CB}\\{PB=PB}\\{AP=CP}\end{array}\right.$,
∴△ABP≌△CBP,
∴∠ABP=∠CBP=45°,
过P作PE⊥BC于E,
∴PE=BE,
∵BC=4$\sqrt{2}$,
∴CE=4$\sqrt{2}$-PE,
在Rt△PCE中,PC2=PE2+CE2,
即(2$\sqrt{5}$)2=PE2+(4$\sqrt{2}$-PE)2,
∴PE=3$\sqrt{2}$或$\sqrt{2}$,
∴PB=$\sqrt{2}$PE=6或2.
故答案为:6或2.
点评 本题考查了正方形的性质,全等三角形的判断和性质,等腰直角三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键,

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
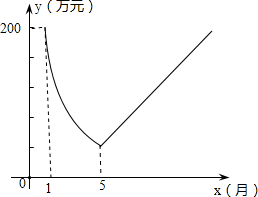 我省某化工厂2013年1月的利润为200万元,若设2013年1月为第一个月,第x个月的利润为y万元;由于污染问题,该厂决定从2013年1月底适当限产,并投入资金进行新技术改造,导致月利润明显下降.从1月底到5月,y与x成反比例关系.到5月底,新技术改造任务顺利完成,从这时起,该厂每月利润比前月增加20万元(如图).
我省某化工厂2013年1月的利润为200万元,若设2013年1月为第一个月,第x个月的利润为y万元;由于污染问题,该厂决定从2013年1月底适当限产,并投入资金进行新技术改造,导致月利润明显下降.从1月底到5月,y与x成反比例关系.到5月底,新技术改造任务顺利完成,从这时起,该厂每月利润比前月增加20万元(如图). 如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).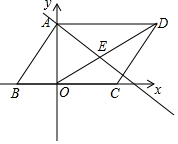 如图,平行四边形ABCD在直角坐标系中,tan∠ABC=$\frac{4}{3}$,AD=6,OA的长是方程x2-x-12=0的一个根,E是线段OD的中点.
如图,平行四边形ABCD在直角坐标系中,tan∠ABC=$\frac{4}{3}$,AD=6,OA的长是方程x2-x-12=0的一个根,E是线段OD的中点.