题目内容
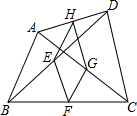 如图,在四边形ABCD中,点E,F,G,H分别是边BD,BC,AC,DA的中点,如果四边形EFGH为矩形,那么应在四边形ABCD中添加一个条件
如图,在四边形ABCD中,点E,F,G,H分别是边BD,BC,AC,DA的中点,如果四边形EFGH为矩形,那么应在四边形ABCD中添加一个条件考点:中点四边形
专题:
分析:矩形的判别方法是说明一个四边形为矩形的理论依据,常用三种方法:
①定义;
②四角相等;
③对角线相等.
①定义;
②四角相等;
③对角线相等.
解答:解:条件是AC⊥BD.
∵EH、GF分别是△ABC、△BCD的中位线,
∴EH∥=
BC,GF∥=
BC,
∴EH∥=GF,
∴四边形EFGH是平行四边形.
要使四边形EFGH是矩形,则要使EH⊥GH,这样,AC⊥BD,
∴GH⊥GF,
∴四边形EFGH是矩形.
故答案为:AC⊥BD.
∵EH、GF分别是△ABC、△BCD的中位线,
∴EH∥=
| 1 |
| 2 |
| 1 |
| 2 |
∴EH∥=GF,
∴四边形EFGH是平行四边形.
要使四边形EFGH是矩形,则要使EH⊥GH,这样,AC⊥BD,
∴GH⊥GF,
∴四边形EFGH是矩形.
故答案为:AC⊥BD.
点评:此题主要考查三角形的中位线定理和矩形的判定,解题的关键是了解矩形的判定定理.

练习册系列答案
相关题目
 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )| A、a-b>0 |
| B、|a|-|b|>0 |
| C、ab>0 |
| D、a+b>0 |
过点A(2,-3)且垂直于y轴的线段交y轴于点B,则AB的长为( )
| A、2 | B、-2 | C、3 | D、-3 |
△ABC中,AB=AC,∠A=40°,BD是高,则∠DBC=( )
| A、40° | B、20° |
| C、70° | D、35° |
 如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=9cm,BD=6cm,那么点D到直线AB的距离是
如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=9cm,BD=6cm,那么点D到直线AB的距离是 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE于点F.