题目内容
16.已知关于x的方程x2+mx+m-3=0.(1)若该方程的一个根为1,求m的值及该方程的另一根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
分析 (1)把x=1代入原方程求得m的值,进一步求得方程的另一个根即可;
(2)计算出根的判别式,进一步利用配方法和非负数的性质证得结论即可.
解答 (1)解:把x=1代入方程x2+mx+m-3=0得
1+m+m-3=0,
解得:m=1,
则原方程为x2+x-2=0,
解得:x=-2,或x=1.
因此方程的另一个根为-2.
(2)证明:△=m2-4(m-3)=(m-2)2+8,
∵(m-2)2≥0,
∴(m-2)2+8>0,
∴该方程都有两个不相等的实数根.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
7.二元一次方程2y-x=1有无数多个解,下列四组值中是该方程的解的是( )
| A. | $\left\{\begin{array}{l}{x=0}\\{y=-\frac{1}{2}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ |
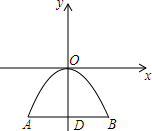 一座石拱桥的桥拱是近似的抛物线形.建立如图所示的坐标系,其函数关系式为
一座石拱桥的桥拱是近似的抛物线形.建立如图所示的坐标系,其函数关系式为 如图是将正方体切去一块后的几何体,则这个几何体的俯视图是( )
如图是将正方体切去一块后的几何体,则这个几何体的俯视图是( )




