题目内容
17.若二元一次方程组$\left\{\begin{array}{l}{ax-2016y=2015}\\{2016x-by=2017}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,则二元一次方程组$\left\{\begin{array}{l}{a(x-y)-2016(x+y)=2015}\\{2016(x-y)-b(x+y)=2017}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{1}{2}}\end{array}\right.$ |
分析 根据题意将x,y的值代入方程组$\left\{\begin{array}{l}{ax-2016y=2015}\\{2016x-by=2017}\end{array}\right.$,得出关于a,b的二元一次方程组,求得a、b的值,然后代入方程组$\left\{\begin{array}{l}{a(x-y)-2016(x+y)=2015}\\{2016(x-y)-b(x+y)=2017}\end{array}\right.$,解方程组求出即可.
解答 解:∵二元一次方程组$\left\{\begin{array}{l}{ax-2016y=2015}\\{2016x-by=2017}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2a-2016=2015}\\{4032-b=2017}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2015.5}\\{b=2015}\end{array}\right.$,
代入方程组$\left\{\begin{array}{l}{a(x-y)-2016(x+y)=2015}\\{2016(x-y)-b(x+y)=2017}\end{array}\right.$得$\left\{\begin{array}{l}{2015.5(x-y)-2016(x+y)=2015}\\{2016(x-y)-2015(x+y)=2017}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$
故选C.
点评 此题主要考查了二元一次方程组的解法,熟练掌握二元一次方程组的解法是解题关键.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
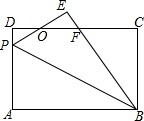 如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )
如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )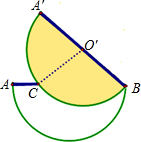 将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,$\widehat{AB}$与直径AB交于点C,连接点C与圆心O′.
将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,$\widehat{AB}$与直径AB交于点C,连接点C与圆心O′.