题目内容
15.△ABC中,∠C=90°,AB=3cm,BC=2cm,以A为圆心,以2.3cm为半径作圆,则C点和⊙A的关系是点C在圆外.分析 根据题意画出图形,利用勾股定理求出AC的长,再根据点与圆的位置关系即可得出结论.
解答  解:如图所示,
解:如图所示,
∵△ABC中∠C=90°,AB=3cm,BC=2cm,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∵2.3>$\sqrt{5}$,
∴点C在圆外.
故答案为:点C在圆外.
点评 本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.在⊙O中,r=13,弦AB=24,则圆心O到AB的距离为( )
| A. | 5 | B. | 10 | C. | 12 | D. | 13 |
20.用配方法解关于x的方程x2-6x+5=0时,此方程可变形为( )
| A. | (x+3)2=4 | B. | (x+3)2+4=0 | C. | (x-3)2=4 | D. | (x-3)2+4=0 |
 如图,直线AB是一次函数y=kx+b的图象,求这个函数的关系式.
如图,直线AB是一次函数y=kx+b的图象,求这个函数的关系式.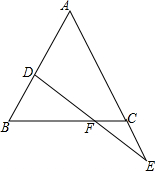 如图:△ABC中AB=AC,在AB边上截取BD,在AC的延长线上截取CE,使CE=BD.连接ED交BC于F.问:DF与EF相等吗?如果相等,请证明;如果不相等,请说明理由.
如图:△ABC中AB=AC,在AB边上截取BD,在AC的延长线上截取CE,使CE=BD.连接ED交BC于F.问:DF与EF相等吗?如果相等,请证明;如果不相等,请说明理由.