题目内容
在矩形 ABCD 中,AB=3,BC=4,E,F 是对角线 ACS 行的两个动点,分别从 A,C 同时出发 相向而行,速度均为 1cm/s,运动时间为 t 秒,当其中一个动点到达后就停止运动.
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 始终是平行四边形. 在(1)条件下,当 t 为何值时,四边形 EGFH 为矩形.
(3)若 G,H 分别是折线 A﹣B﹣C,C﹣D﹣A 上的动点,与 E,F 相同的速度同时出发,当 t 为何 值时,四边形 EGFH 为菱形.

【考点】四边形综合题.
【分析】(1)由矩形的性质得出 AB=CD,AB∥CD,AD∥BC,∠B=90°,由勾股定理求出 AC=5, 由 SAS 证明△AFG≌△CEH,得出 GF=HE,同理得出 GE=HF,即可得出结论;
先证明四边形 BCHG 是平行四边形,得出 GH=BC=4,当对角线 EF=GH=4 时,平行四边形 EGFH
是矩形,分两种情况:①AE=CF=t,得出 EF=5﹣2t=4,解方程即可;②AE=CF=t,得出 EF=5﹣2
(5﹣t)=4,解方程即可;
(3)连接 AG、CH,由菱形的性质得出 GH⊥EF,OG=OH,OE=OF,得出 OA=OC,AG=AH,证 出四边形 AGCH 是菱形,得出 AG=CG,设 AG=CG=x,则 BG=4﹣x,由勾股定理得出方程,解方
程求出 BG,得出 AB+BG= ,即可得出 t 的值.
,即可得出 t 的值.
【解答】(1)证明:∵四边形 ABCD 是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=  =5,∠GAF=∠HCE,
=5,∠GAF=∠HCE,
∵G,H 分别是 AB,DC 中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
 ∴AF=CE,
∴AF=CE,
在△AFG 和△CEH 中, ,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形 EGFH 是平行四边形. 解:由(1)得:BG=CH,BG∥CH,
∴四边形 BCHG 是平行四边形,
∴GH=BC=4,当 EF=GH=4 时,平行四边形 EGFH 是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4, 解得:t=0.5;
②AE=CF=t,EF=5﹣2(5﹣t)=4, 解得:t=4.5;
综上所述:当 t 为 0.5s 或 4.5s 时,四边形 EGFH 为矩形.
(3)解:连接 AG、CH,如图所示:
∵四边形 EGFH 为菱形,
∴GH⊥EF,OG=O H,OE=OF,
H,OE=OF,
∴OA=OC,AG=AH,

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案 ,若
,若 的面积分别为1和9,
的面积分别为1和9, 的面积为
的面积为


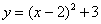 的顶点坐标是( )
的顶点坐标是( )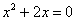 的根是 .
的根是 .