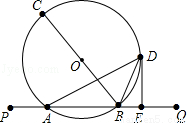
题目内容
如图所示，MN是圆O中一条固定的弦，劣弧MN的度数为1200，点C是圆O上一个动点（不与M、N重合）。连接MC、NC，D、E分别是NC和MC的中点，直线DE交圆O于点A、B。已知圆O的半径为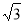
，那么在点C的运动过程中AE+BD的最小值为 。
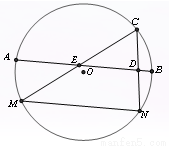
【解析】
试题解析：【解析】
如下图所示，
∵点D、E分别是NC、MC的中点，
∴点C在劣弧MN的中点时，AB的长度最小，
此时DE＝
MN，连接OA、OM，连接OC与MN、AB分别交于点F、G，
∵劣弧MN的度数是120°，
∴∠OMN＝
（180°－120°）＝30°，
∵⊙的半径是
，
∴OF＝OM＝
，MF＝×
＝
，
∵D、E分别是NC、MC的中点，
∴FG＝（OC－OF）＝
＝
，
∴OG＝OF＋FG＝
＝
，
在Rt△AOG中，AG＝
＝
＝
，
∴AE＋BD＝2AG－DE＝2×－＝.
考点：三角形的中位线定理、勾股定理、圆心角、弧、弦的关系
点评：本题主要考查了三角形的中位线定理、勾股定理、圆心角、弧、弦的关系，解决本题的关键是判断出当点C在劣弧MN的中点时AE＋BD的值最小.
练习册系列答案
阅读快车系列答案
相关题目
B．
C．
D．
）。 
某地民政部门举行“关爱留守儿童”主题福利彩票销售活动，发行10万张（每张彩票2元），募集到的资金全部用于当地留守儿童营养改善计划。这些彩票奖项设置如下表：
奖金（元） | 10000 | 5000 | 1000 | 500 | 100 | 50 |
数量（张） | 1 | 4 | 20 | 40 | 100 | 200 |
小明花2元购买一张彩票，他中奖的奖金不少于1000元的概率是 。
