题目内容
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
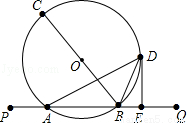
(1)求证:DE与⊙O相切;
(2)连结AD,己知BC=10,BE=2,求sin∠BAD的值.
(1)证明:连结OD,如图,
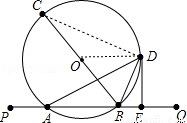
∵BD平分∠CBQ交⊙O于点D,
∴∠CBD=∠QBD,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠QBD,
∴OD∥BQ,
∵DE⊥PQ,
∴OD⊥DE,
∴DE与⊙O相切;
(2)【解析】
∵BC是⊙O的直径,
∴∠BDC=90°,
∵DE⊥AB,
∴∠BED=90°,
∵∠CBD=∠QBD,
∴Rt△BCD∽△BDE,
∴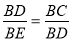 ,即
,即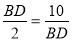 ,
,
∴BD=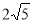 ,
,
在Rt△BCD中,sin∠C=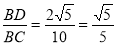 ,
,
∵∠BAD=∠C,
∴sin∠BAD=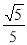 .
.
【解析】
试题分析:(1)连结OD,利用角平分线的定义得∠CBD=∠QBD,而∠OBD=∠ODB,则∠ODB=∠QBD,于是可判断OD∥BQ,由于DE⊥PQ,根据平行线的性质得OD⊥DE,则可根据切线的判定定理得到DE与⊙O相切;
(2)连结CD,根据圆周角定理由BC是⊙O的直径得到∠BDC=90°,再证明Rt△BCD∽△BDE,利用相似比可计算出BD=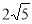 ,在Rt△BCD中,根据正弦的定义得到sin∠C=
,在Rt△BCD中,根据正弦的定义得到sin∠C=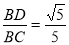 ,然后根据圆周角定理得∠BAD=∠C,即有sin∠BAD=
,然后根据圆周角定理得∠BAD=∠C,即有sin∠BAD=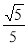
考点:切线的判定;锐角三角函数的定义

练习册系列答案
相关题目
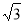 ,那么在点C的运动过程中AE+BD的最小值为 。
,那么在点C的运动过程中AE+BD的最小值为 。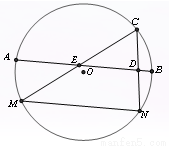

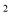 =50 B.20(1﹣x)
=50 B.20(1﹣x) =50
=50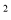 =20 D.50(1﹣x)
=20 D.50(1﹣x) =20
=20
 BC;
BC; 的自变量的取值范围是 .
的自变量的取值范围是 .