题目内容
如图,将圆C放置在直角坐标系中,圆C经过原点O以及点A(2,0),点B(0, )。
)。

(1)求圆心的坐标以及圆C的半径; (4分)
(2)设弧OB的中点为D,请求出同时经过O,A,D三个点的抛物线解析式。
并判断该抛物线的顶点是否在圆C上,说明理由。(6分)
(3)若(2)中的抛物线上存在点P(m,n),满足∠APB为钝角,直接写出m的取值范围。(2分)
(1)点C的坐标是(1, );
);
(2)顶点不在圆C上;
(3)-1<m<0或2<x<3.
【解析】
试题解析:【解析】
∵∠AOB=90°,
∴AB为圆直径
∵点A(2,0),点B(0, )
)
∴AB=
∴⊙O的半径是2,
过点C作CN⊥OA垂足为N点,
∴N是OA中点
∴CN= OB=
OB= ,ON=1
,ON=1
∴点C的坐标是(1, );
);

(2)如下图所示,
连接OD交OB于点M
∴CD⊥OB于点M
∴CM= OA=1
OA=1
∴MD=1
∴点D的坐标为(-1, )
)
∵抛物线经过原点O,
∴设所求抛物线的解析式为
把点D(-1, )、A(2,0)代入解析式得:
)、A(2,0)代入解析式得:

解得
∴抛物线解析式为:
配方得: ,
,
∴抛物线的顶点坐标是(1, )
)
该点到圆心C的距离是
所以顶点不在圆C上;

(3)∵AB是圆的直径,
∴当抛物线上的点在圆内部时,∠APB是钝角,
∴m的取值范围是-1<m<0或2<x<3.
考点:二次函数解析式的求法、圆的基本性质
点评:本题主要考查了二次函数解析式的求法与圆的基本性质.求二次函数的解析式的常用方法是待定系数法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,垂足点为
,垂足点为 ,若
,若 ,则
,则 =______________.
=______________.
 ; -
; - ____-
____- ;
;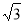 ,那么在点C的运动过程中AE+BD的最小值为 。
,那么在点C的运动过程中AE+BD的最小值为 。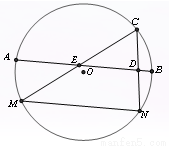
 。
。