题目内容
已知如图，△ABC是等边三角形，P是三角形外的一点，且∠ABP+∠ACP=180°．
求证：AP平分∠BPC．
把△APC以点A为旋转中心顺时针旋转60°得到△ABP'
所以△APC≌△ABP'
∴∠APC=∠AP'B ,AP'=AP
∠ACP=∠ABP'
∵∠ABP+∠ACP=180°
∴∠ABP+∠ABP'=180°即P'BP为直线
又∵ AP'=AP
∠AP’B=∠APB
∴∠APB=∠APC
即AP平分∠BPC
解析
练习册系列答案
相关题目
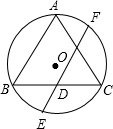已知如图，△ABC是⊙O的内接正三角形，弦EF经过BC边的中点D，且EF∥BA，若⊙O的半径为4
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
22、已知如图，△ABC是等腰直角三角形，∠C为直角．
已知如图，△ABC是等边三角形，E、G是AB边的三等分点，F、H是AC边的三等分点，则图中阴影部分的面积是△ABC的面积的（ ）
已知如图，△ABC是等边三角形，P是三角形外的一点，且∠ABP+∠ACP=180°．