题目内容
已知如图,△ABC是等边三角形,边长为6,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,求AD的长.
分析:先由△ABC是等边三角形求得△DEF为等边三角形,再利用,△ADF≌△DEB≌△EFC,和勾股定理即可求出答案.
解答:解:由△ABC是等边三角形得,∠ABC=∠ACB=∠BAC=60°
又∵DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,
∴△DEF为等边三角形,
∴△ADF≌△DEB≌△EFC,
∴AD=BE=CF,
∵FD⊥AB,∠AFD=30°,
∴AD=
=
,
解得:AD=2.
答:AD的长为2.
又∵DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,
∴△DEF为等边三角形,
∴△ADF≌△DEB≌△EFC,
∴AD=BE=CF,
∵FD⊥AB,∠AFD=30°,
∴AD=
| AF |
| 2 |
| AC-CF |
| 2 |
解得:AD=2.
答:AD的长为2.
点评:此题考查学生对等腰三角形的判定与性质和等边三角形的性质的理解和掌握,还涉及到直角三角形的特点,此题的关键是先求证△DEF为等边三角形,然后利用勾股定理求得的.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
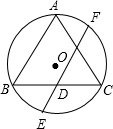 已知如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥BA,若⊙O的半径为
已知如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥BA,若⊙O的半径为4
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 22、已知如图,△ABC是等腰直角三角形,∠C为直角.
22、已知如图,△ABC是等腰直角三角形,∠C为直角. 已知如图,△ABC是等边三角形,E、G是AB边的三等分点,F、H是AC边的三等分点,则图中阴影部分的面积是△ABC的面积的( )
已知如图,△ABC是等边三角形,E、G是AB边的三等分点,F、H是AC边的三等分点,则图中阴影部分的面积是△ABC的面积的( ) 已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.
已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.