题目内容
已知m是方程x2-x-3=0的一个实数根,则代数式(m2-m)(m-
+1)的值为 .
| 3 |
| m |
考点:一元二次方程的解
专题:
分析:把x=m代入已知方程,得到m2-m=3,m2-3=m,然后代入所求的代数式进行求值即可.
解答:解:∵m是方程x2-x-3=0的一个实数根,
∴m2-m-3=0,
∴m2-m=3,m2-3=m,
∴(m2-m)(m-
+1)=3×(
+1)=3×(1+1)=6.
故答案是:6.
∴m2-m-3=0,
∴m2-m=3,m2-3=m,
∴(m2-m)(m-
| 3 |
| m |
| m2-3 |
| m |
故答案是:6.
点评:本题考查了一元二次方程的解的定义.注意“整体代入”思想的应用.

练习册系列答案
相关题目
在实数
,
,0.1414,
,-
,0.1010010001…,-
,0,1-
,
,|
-1|中,有几个无理数( )
| π |
| 2 |
| 22 |
| 7 |
| 3 | 9 |
| 5 |
| 2 |
|
| 2 |
| ||
| 2 |
| 4 |
| A、3个 | B、4个 | C、5个 | D、6个 |
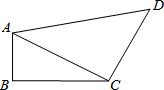 如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且∠ABC=90°,连接AC.
如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且∠ABC=90°,连接AC. 如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.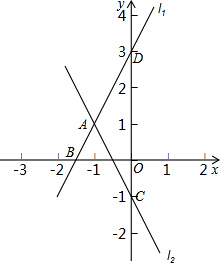 已知直线L1:y1=2x+3与直线L2:y2=kx-1交于A点,A点横坐标为-1,且直线L1与x轴交于B点,与y轴交于D点,直线L2与y轴交于C点.
已知直线L1:y1=2x+3与直线L2:y2=kx-1交于A点,A点横坐标为-1,且直线L1与x轴交于B点,与y轴交于D点,直线L2与y轴交于C点.