题目内容
 如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.考点:等腰三角形的性质
专题:
分析:AB=AC=CD,AD=BD可得∠B=∠C=∠BAD,∠CDA=∠CAD,且利用外角可得∠CDA=2∠B=2∠C,在△ACD中利用三角形内角和可求得∠C,进一步可求得∠CAC,再利用角的和差求得∠BAC.
解答:解:
∵AB=AC,DA=DB,
∴∠B=∠C=∠BAD,
∵CA=CD,
∴∠CDA=∠CAD,
又∠CDA=∠B+∠BAD=2∠B=2∠C,
∴∠CAD=2∠C,
在△ACD中,∠C+∠CDA+∠CAD=180°,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=2∠C=72°,
∴∠BAC=∠BAD+∠CAD=36°+72°=108°.
∵AB=AC,DA=DB,
∴∠B=∠C=∠BAD,
∵CA=CD,
∴∠CDA=∠CAD,
又∠CDA=∠B+∠BAD=2∠B=2∠C,
∴∠CAD=2∠C,
在△ACD中,∠C+∠CDA+∠CAD=180°,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=2∠C=72°,
∴∠BAC=∠BAD+∠CAD=36°+72°=108°.
点评:本题主要考查等腰三角形的性质及外角性质、三角形内角和定理,由条件得到2∠C+2∠C+∠C=180°求出∠C是解题的关键,注意外角性质及三角形内角和定理的应用.

练习册系列答案
相关题目
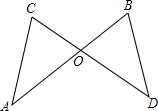 如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )| A、1 | B、3 | C、4 | D、5 |
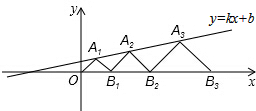 在平面直角坐标系xOy中,点A1,A2,A3…和B1,B2,B3…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
在平面直角坐标系xOy中,点A1,A2,A3…和B1,B2,B3…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2( 如图,在Rt△ABC中,∠C=90°,AC=BC=a,延长CA到D,使AD=AB,连接BD.
如图,在Rt△ABC中,∠C=90°,AC=BC=a,延长CA到D,使AD=AB,连接BD.