题目内容
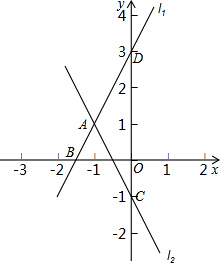 已知直线L1:y1=2x+3与直线L2:y2=kx-1交于A点,A点横坐标为-1,且直线L1与x轴交于B点,与y轴交于D点,直线L2与y轴交于C点.
已知直线L1:y1=2x+3与直线L2:y2=kx-1交于A点,A点横坐标为-1,且直线L1与x轴交于B点,与y轴交于D点,直线L2与y轴交于C点.(1)直线L2的解析式;
(2)直接写出当y1≤y2时,自变量x的取值范围;
(3)连结BC,求出S△ABC;
(4)在直线L1上是否存在点P,使得S△BCP=2S△ABC?若存在,请求出点P的坐标;
(5)在y轴上是否存在一点Q,使得S△BCQ=2S△ABC?若存在,请求出点Q的坐标;
(6)在y轴上是否存在一点R,使得S△ABR=2S△ABC?若存在,请求出点R的坐标.
考点:两条直线相交或平行问题
专题:
分析:(1)根据A点在直线l1上,且横坐标为-1,求出A点的坐标,再根据直线l2过A点,将(-1,1)代入直线l2解析式,即可求出答案;
(2)根据图象即可求得;
(3)根据已知得出B点的坐标,再根据l1与y轴交于D点,得出D点和C点的坐标,再根据三角形的面积公式得出S△ABC.
(4)由于△ABC、△BCP同高,根据已知得出B是AP的中点或A是PB的中点,根据线段中点的求法即可求得;
(5)设Q(0,y),根据S△BCQ=
CQ•OB即可求得;
(6)设C到直线L1的距离为h1,R到直线L1的距离为h2,根据
=
,即可求得DR,进而即可求得R的坐标.
(2)根据图象即可求得;
(3)根据已知得出B点的坐标,再根据l1与y轴交于D点,得出D点和C点的坐标,再根据三角形的面积公式得出S△ABC.
(4)由于△ABC、△BCP同高,根据已知得出B是AP的中点或A是PB的中点,根据线段中点的求法即可求得;
(5)设Q(0,y),根据S△BCQ=
| 1 |
| 2 |
(6)设C到直线L1的距离为h1,R到直线L1的距离为h2,根据
| h1 |
| DC |
| h2 |
| DR |
解答:解:(1)∵y1=2x+3过A点,A点横坐标为-1,
∴y1=-2+3=1,
∴A(-1,1),
把A(-1,1)代入y2=kx-1得,1=-k-1,解得k=-2,
∴直线L2的解析式为y2=-2x-1.
(2)由图象可得x≤-1时,y1≤y2,
(3)L1与x轴交于B点,则B点坐标为(-
,0),L1与y轴交于D点,
则D点坐标为(0,3),L2与y轴交于C点,则C点坐标为(0,-1),
S△ABC=S△BCD-S△ACD=
CD•|xB|-
CD•|xA|=1;
(4)存在;
由于△ABC、△BCP同高,若S△BCP=2S△ABC,则BP=2AB,
∴B是AP的中点或A是PB的中点,
∵A(-1,1),B(-
,0),
∴P(-2,-1)或(-
,2);
(5)设Q(0,y),
∵S△ABC=1,S△BCQ=2S△ABC,
∴S△BCQ=
CQ•OB=
|y+1|×
=2×1,解得y=-
或y=
,
∴Q(0,-
)或(0,
).
(6)设C到直线L1的距离为h1,
∵A(-1,1),B(-
,0),
∴AB=
=
∵S△ABC=
AB•h1=1,
∴h1=
,
∵S△ABR=2S△ABC,由于△ABC、△ABR同底,
∴设R到直线L1的距离为h2=
,
∴
=
,
即
=
,解得DR=8,
∴R(0,-5)或(0,11).
∴y1=-2+3=1,
∴A(-1,1),
把A(-1,1)代入y2=kx-1得,1=-k-1,解得k=-2,
∴直线L2的解析式为y2=-2x-1.
(2)由图象可得x≤-1时,y1≤y2,
(3)L1与x轴交于B点,则B点坐标为(-
| 3 |
| 2 |
则D点坐标为(0,3),L2与y轴交于C点,则C点坐标为(0,-1),
S△ABC=S△BCD-S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
(4)存在;
由于△ABC、△BCP同高,若S△BCP=2S△ABC,则BP=2AB,
∴B是AP的中点或A是PB的中点,
∵A(-1,1),B(-
| 3 |
| 2 |
∴P(-2,-1)或(-
| 1 |
| 2 |
(5)设Q(0,y),
∵S△ABC=1,S△BCQ=2S△ABC,
∴S△BCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 11 |
| 3 |
| 5 |
| 3 |
∴Q(0,-
| 11 |
| 3 |
| 5 |
| 3 |
(6)设C到直线L1的距离为h1,
∵A(-1,1),B(-
| 3 |
| 2 |
∴AB=
(-
|
| ||
| 2 |
∵S△ABC=
| 1 |
| 2 |
∴h1=
4
| ||
| 5 |
∵S△ABR=2S△ABC,由于△ABC、△ABR同底,
∴设R到直线L1的距离为h2=
8
| ||
| 5 |
∴
| h1 |
| DC |
| h2 |
| DR |
即
| ||||
| 4 |
| ||||
| DR |
∴R(0,-5)或(0,11).
点评:本题考查了两直线平行或相交问题,要注意利用一次函数的特点,列出方程,求出未知数再求得解析式;求三角形的面积时找出高和底边长即可.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
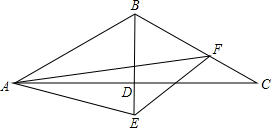 已知,△ABC中,BA=BC,∠ABC=120°,BE⊥AC,垂足D,AF平分∠BAE交BC于F.求证:∠AFE=30°.
已知,△ABC中,BA=BC,∠ABC=120°,BE⊥AC,垂足D,AF平分∠BAE交BC于F.求证:∠AFE=30°.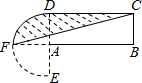 设计一个商标图案,如图6-2阴影部分,其中A为半圆DEF的圆心,BC=a,AB=b.
设计一个商标图案,如图6-2阴影部分,其中A为半圆DEF的圆心,BC=a,AB=b.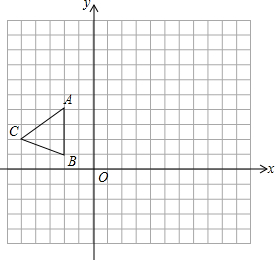 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2). 已知:如图,AD∥BE∥CF.若AB=4,BC=6,DE=5,求DF.
已知:如图,AD∥BE∥CF.若AB=4,BC=6,DE=5,求DF.