Question

6．如图，Rt△ABC中，∠ACB=90°．
（1）作∠BAC的平分线，交BC于点D；（要求：尺规作图，不写作法，保留作图痕迹）
（2）在（1）的条件下，若BD=5，CD=3，求AC的长．

Answer 1

分析 （1）首先以A为圆心，小于AC长为半径画弧，交AC、AB于H、F，再分别以H、F为圆心，大于$\frac{1}{2}$HF长为半径画弧，两弧交于点M，再画射线AM交CB于D；
（2）过点D作DE⊥AB，垂足为E，首先证明△ACD≌△AED可得AC=AE，CD=DE=3，在Rt△BDE中，由勾股定理得：DE²+BE²=BD²，进而可得BE长，然后再在Rt△ABC中，设AC=x，则AB=AE+BE=x+4，利用勾股定理可得x²+8²=（x+4）²，再解即可．

解答 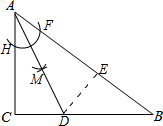解：（1）如图：

（2）过点D作DE⊥AB，垂足为E．则∠AED=∠BED=90°．
∵AD平分∠BAC，
∴∠CAD=∠EAD．
在△ACD和△AED中，$\left\{\begin{array}{l}{∠CAD=∠EAD}\\{∠ACD=∠AED}\\{AD=AD}\end{array}\right.$，
∴△ACD≌△AED（AAS）．
∴AC=AE，CD=DE=3．
在Rt△BDE中，由勾股定理得：DE²+BE²=BD²．
∴BE²=BD²-DE²=5²-3²=16．
∴BE=4．
在Rt△ABC中，设AC=x，则AB=AE+BE=x+4．
由勾股定理得：AC²+BC²=AB²，
∴x²+8²=（x+4）²．
解得：x=6，
即AC=6．

点评 此题主要考查了基本作图，以及勾股定理的应用，全等三角形的判定和性质，关键是得到AC=AE，CD=DE，掌握直角三角形中，两直角边的平方和等于斜边的平方．