题目内容
已知（m+n）2=25，（m-n）2=9，则mn与m2+n2的值分别为（ ）
| A、4，17 | B、3，16 |
| C、5，34 | D、6，18 |
考点：完全平方公式
专题：计算题
分析：先根据完全平方公式展开得到m2+2mn+n2=25，m2-2mn+n2=9，再把两等式相减可计算出mn，然后把mn的值代入其中一个等式可计算出m2+n2的值．
解答：解：∵（m+n）2=25，（m-n）2=9，
∴m2+2mn+n2=25①，m2-2mn+n2=9②，
①-②得4mn=16，
∴mn=4，
∴m2+n2=25-2mn=25-2×4=17．
故选A．
∴m2+2mn+n2=25①，m2-2mn+n2=9②，
①-②得4mn=16，
∴mn=4，
∴m2+n2=25-2mn=25-2×4=17．
故选A．
点评：本题考查了完全平方公式：（a±b）2=a2±2ab+b2．也考查了代数式的变形能力．
练习册系列答案
相关题目
如图，已知点A的坐标为（| 3 |
| k |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
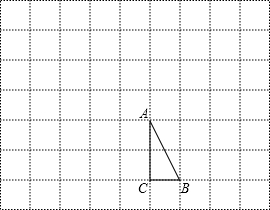如图在7×9的小正方形网格中，△ABC的顶点A、B、C在网格的格点上，将△ABC向左平移3个单位，再向上平移3个单位得到△A′B′C′，将△ABC按一定规律顺次旋转，第1次将△ABC绕点B顺时针旋转90°得到△A1BC1，第2次将△A1BC1绕点A1顺时针旋转90°得到△A1BC2，第3次将△A1BC2绕点C2顺时针旋转90°得到△A2B2C2，第4次将△A2B2C2绕点B2顺时针旋转90°得到△A3B2C3，依次旋转下去．
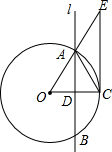如图，直线l与⊙O交于A，B两点，且与半径OC垂直，垂足为点D，连接AC，在线段OA的延长线上取一点E，使AE=AC，连接CE．已知OA=4，∠O=60°如图的几何体，其左视图均为圆的是（ ）
| A、①② | B、②③ | C、③④ | D、①④ |
如图，量一量，算一算．
已知圆柱按如图所示方式放置，其左视图的面积为48，则该圆柱的侧面积为