题目内容
D是△ABC的AC上一点，AD：DC=3：1，G是BD中点，连AG延长线交BC于E，则AE：GE= ．
考点：平行线分线段成比例
专题：计算题
分析：作DF∥AE交BC于F，如图，先利用DF∥AE得到△CFD∽△CEA，则
=
，加上AD：DC=3：1，则AE=4DF，再利用GE∥DF得△BEG∽△BFD，则
=
，
加上G是BD中点得到GE=
DF，然后计算
．
| DF |
| AE |
| CD |
| CA |
| GE |
| DF |
| BG |
| BD |
加上G是BD中点得到GE=
| 1 |
| 2 |
| AE |
| GE |
解答：
解：作DF∥AE交BC于F，如图，
∵DF∥AE，
∴△CFD∽△CEA，
∴
=
，
而AD：DC=3：1，
∴
=
，即AE=4DF，
∵GE∥DF，
∴△BEG∽△BFD，
∴
=
，
而G是BD中点，即BG=
BD，
∴
=
，即GE=
DF，
∴
=
=8．
故答案为8：1．
解：作DF∥AE交BC于F，如图，∵DF∥AE，
∴△CFD∽△CEA，
∴
| DF |
| AE |
| CD |
| CA |
而AD：DC=3：1，
∴
| DF |
| AE |
| 1 |
| 4 |
∵GE∥DF，
∴△BEG∽△BFD，
∴
| GE |
| DF |
| BG |
| BD |
而G是BD中点，即BG=
| 1 |
| 2 |
∴
| GE |
| DF |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AE |
| GE |
| 4DF | ||
|
故答案为8：1．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
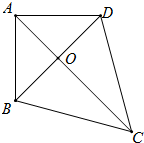如图，BA⊥AD，∠ADB=∠ABD=∠DAO，∠DBC=60°，∠DCO=∠BCO．
在同一条公路旁，住着五个人，他们在同一家公司上班，如图所示，不妨设这五个人的家分别住在点A，B，D，E，F的位置，公司在点C，若AB=5km，BC=3km，CD=3km，DE=2km，EF=1km，他们全部乘出租车上、下班，车费单位报销，出租车收费标准是：起步价3元（3km以内，包括3km）以后每千米1.5元（不足1km，以1km计算）．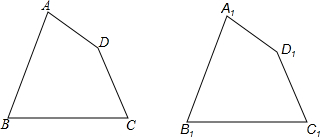
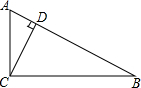如图，Rt△ABC中，∠ACB=90°，CD⊥AB于D