Question

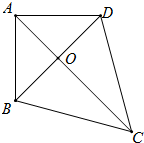如图，BA⊥AD，∠ADB=∠ABD=∠DAO，∠DBC=60°，∠DCO=∠BCO．
（1）求证：BD⊥AC；
（2）求∠DCO的度数；
（3）求证：BC=DC．

Answer 1

考点：等腰三角形的判定与性质,三角形内角和定理

专题：

分析：（1）由条件可求得∠ABD=∠DAO=45°，可证得结论；
（2）结合条件且∠DBC=60°，可求得∠DCO；
（2）利用垂直平分线性质可证明BC=DC．

解答：（1）证明：
∵BA⊥AD，
∴∠BAD=90°，
∴∠ABD=∠ADB=45°，
∴∠DAO=45°，
∴∠AOD=90°，
∴BD⊥AC；
（2）解：
∵∠DCO=∠BCO，且∠DBC=60°，
∴∠DCO=∠BCO=30°；
（3）证明：
由（1）可知O为BD中点，且AC⊥BD，
∴AC垂直平分BD，
∴BC=DC．

点评：本题主要考查等腰三角形的性质和判定，掌握等角对等边、等边对等角是解题的关键．注意三角形内角和定理的应用．