Question

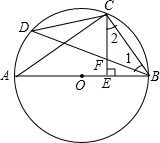
如图，AD是⊙O的弦，AB经过圆心O，交⊙O于点C，∠BAD=∠B=30°．
（1）求证：BD是⊙O的切线；
（2）若⊙O的半径为6，求图中阴影部分的面积．

Answer 1

考点：切线的判定,扇形面积的计算

专题：

分析：（1）连接OD，求出∠ODB=90°，根据切线的判定推出即可；
（2）求出BD，分别求出三角形ODB和扇形ODC的面积，即可求出答案．

解答：（1）证明：连接OD，
∵OA=OD，∠BAD=30°，
∴∠ADO=∠BAD=30°，
∴∠DOB=∠A+∠ADO=30°+30°=60°，
∵∠B=30°，
∴∠ODB=180°-60°-30°=90°，
即OD⊥BD，
∴BD是⊙O的切线；

（2）解：∵∠B=30°，∠ODB=90°，OD=6，
∴OB=2OD=12，由勾股定理得：BD=

OB2-OD2

=

122-62

=6

3

，
∴阴影部分的面积S=S_△OBD-S_扇形ODC=

1

2

×6×6

3

-

60π•62

360

=18

3

-6π．

点评：本题考查了等腰三角形性质，三角形外角性质，扇形面积，三角形面积，切线的判定的应用，题目比较好，难度适中．