Question

9．如图，AC是四边形ABCD的对角线，∠B=90°，∠ADC=∠ACB+45°，BC=AB+$\sqrt{3}$，若AC=CD，则边AD的长为$\sqrt{6}$．

Answer 1

分析 作∠DCH=∠ACB，并过D作DH⊥CH于H，延长HD交BA延长线于K，由AAS证明△ABC≌△DHC，得出BC=HC，AB=DH，证出四边形BCKH是正方形，得出∠K=90°，BK=HK，由已知条件得出AK=DK=BC-AB=$\sqrt{3}$，△ADK是等腰直角三角形，由勾股定理求出AD即可．

解答 解：作∠DCH=∠ACB，并过D作DH⊥CH于H，延长HD交BA延长线于K，如图所示：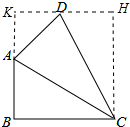
设∠DCH=∠ACB=x，
∵AC=CD，
∴∠DAC=∠ADC=x+45°，
∴∠ACD=180°-2（x+45°）=90°-2x，
∴∠BCH=90°，
在△ABC和△DHC中，
$\left\{\begin{array}{l}{∠ACB=∠DCH}&{\;}\\{∠B=∠DHC=90°}&{\;}\\{AC=DC}&{\;}\end{array}\right.$，
∴△ABC≌△DHC（AAS），
∴BC=HC，AB=DH，
∴四边形BCKH是正方形，
∴∠K=90°，BK=HK，
∴AK=DK=BC-AB=$\sqrt{3}$，
∴△ADK是等腰直角三角形，
∴AD=$\sqrt{A{K}^{2}+D{K}^{2}}$=$\sqrt{6}$．
故答案为：$\sqrt{6}$．

点评 本题考查了全等三角形的判定与性质、正方形的判定与性质、勾股定理等知识；本题综合性强，有一定难度，通过作辅助线证明三角形全等是解决问题的关键．