Question

【题目】已知，如图，点A为⊙O上的一点．

（1）用没有刻度的直尺和圆规作一个⊙O的内接正三角形ABC．（保留作图痕迹并标出B、C）；

（2）若⊙O半径为10，则三角形ABC的面积为　　　　　　．

Answer 1

【答案】（1）答案见解析；（2）．

【解析】分析: （1）以OA为半径，在圆上依次截取得到圆的6等份点，从而得到圆的三等份点，于是可作出⊙O的内接正三角形ABC；

（2）连接OB、OC，延长AO交BC于点D，则AD⊥BC，先求得OD＝BOcos60°＝5，BD＝BOsin60°＝5，据此知BC＝2BD＝10、AD＝AO＋OD＝15，根据三角形的面积公式可得答案．

详解: （1）如图所示，△ABC即为所求：

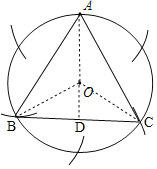
（2）如图，连接OB、OC，延长AO交BC于点D，则AD⊥BC，

∵∠BOC＝2∠BAC＝120°，

∴∠BOD＝60°，

则OD＝BOcos60°＝10×＝5，BD＝BOsin60°＝10×＝5，

∴BC＝2BD＝10、AD＝AO＋OD＝15，

∴S△ABC＝BCAD＝×10×15＝75，

故答案为：75．

点睛: 本题考查了作图复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．