题目内容
【题目】定义：如果一个三角形一条边上的高与这条边的比值是3：5，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．
（概念感知）
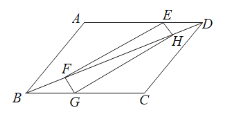
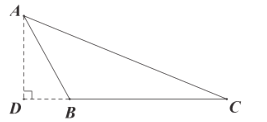
（1）如图1，在
中，
，
，
，试判断是否是“准黄金”三角形，请说明理由．
（问题探究）
（2）如图2，是“准黄金”三角形，BC是“金底”，把沿BC翻折得到
，连AB接AD交BC的延长线于点E，若点C恰好是
的重心，求
的值．
（拓展提升）
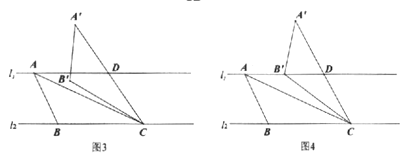
（3）如图3，
，且直线
与
之间的距离为3，“准黄金”的“金底”BC在直线上，点A在直线上．
，若
是钝角，将绕点
按顺时针方向旋转
得到
，线段
交于点D．
①当
时，则
_________；
②如图4，当点B落在直线上时，求
的值．
【答案】（1）
是“准黄金”三角形，理由见解析；（2）
；（3）①
；②
．
【解析】
（1）过点A作
于点D，先求出AD的长度，然后得到
，即可得到结论；
（2）根据题意，由“金底”的定义得
，设
，
，由勾股定理求出AB的长度，根据比值即可求出
的值；
（3）①作AE⊥BC于E，DF⊥AC于F，先求出AC的长度，由相似三角形的性质，得到AF=2DF，由解直角三角形，得到
，则
，即可求出DF的长度，然后得到CD的长度；
②由①可知，得到CE和AC的长度，分别过点
，D作
，
，垂足分别为点G，F，然后根据相似三角形的判定和性质，得到
，然后求出CD和AD的长度，即可得到答案．
解：（1）是“准黄金”三角形．
理由：如图，过点A作于点D，
∵
，
，
∴
．
∴
．
∴是“准黄金”三角形．
（2）∵点A，D关于BC对称，
∴
，
．
∵是“准黄金”三角形，BC是“金底”，
∴．
不防设，，
∵点
为
的重心，
∴
．
∴
，
．
∴
．
∴
．
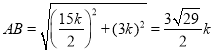（3）①作AE⊥BC于E，DF⊥AC于F，如图：
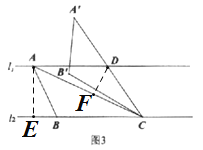
由题意得AE=3，
∵
，
∴BC=5，
∵
，
∴
，
在Rt△ABE中，由勾股定理得：
，
∴
，
∴
；
∵∠AEC=∠DFA=90°，∠ACE=∠DAF，
∴△ACE∽△DAF，
∴
，
设
，则
，
∵∠ACD=30°，
∴
，
∴，
解得：
∴
．
②如图，过点A作
于点E，则
．
∵是“准黄金”三角形，BC是“金底”，
∴．
∴
．
∵，
∴．
∴
．
∴
，
．
分别过点，D作，，垂足分别为点G，F，
∴
，
，
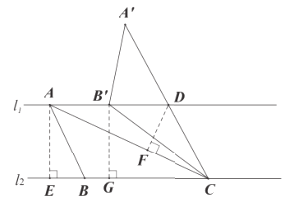
，则
．
∵
，
∴
．
∴
．
∴设
，
，
．
∵
，
∴
，且
．
∴．
∴．
∴
，解得
．
∴
，
．
∴
．
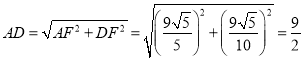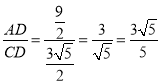